
张晓丹1,2,刘贵忠2,张志禹3,朱 磊1,郭 华1,章为川1
(1.西安工程大学 电子信息学院,陕西 西安 710048; 2.西安交通大学 电子与信息工程学院(微电子学院),陕西 西安 710049; 3.西安理工大学 自动化与信息工程学院,陕西 西安 710048)
摘 要:目前煤田地震勘探的主要难点是深部复杂构造的成像。随着逆时偏移技术的发展,针对煤田地震勘探,如何在保证偏移成像精度的前提下,提高成像计算效率是急需解决的问题之一。从成像区域网格离散化的角度出发,针对高速层过采样和低速夹层采样不足问题,提出赋予研究对象多尺度网格的概念,具有较好的灵活性,能够对同一个地质模型采用疏密结合的方式成像。首先,根据速度模型设计多尺度网格模型,低速区域采用小尺度网格覆盖,高速区域采用大尺度网格覆盖;其次,采用高阶FDTD方法计算多尺度模型内各点的波场值,尤其过渡带内的点;最后,根据成像条件完成地下介质的逆时偏移成像。实验结果表明在保证模拟相同阶数精度条件下,多尺度逆时偏移方法比传统方法计算效率平均提升25.05%。
关键词:煤田地震勘探;多尺度;高阶FDTD;逆时偏移;计算效率
中图分类号:P631
文献标志码:A
文章编号:0253-9993(2018)11-3169-09
ZHANG Xiaodan1,2,LIU Guizhong2,ZHANG Zhiyu3,ZHU Lei1,GUO Hua1,ZHAGN Weichuan1
(1.College of Electronic and Information,Xi’an Polytechnic University,Xi’an 710048,China; 2.College of Electronics and Information Engineering (College of Microelectronics),Xi’an Jiaotong University,Xi’an 710049,China; 3.College of Automation and Information Engineering,Xi’an University of Technology,Xi’an 710048,China)
Abstract:Currently the main difficulties in the coalfield seismic exploration are the image generation on the deep and complex geological structure.With the development of Reverse Time Migration (RTM),it is one of the urgent problem how to improve its efficiency at the same accuracy.From the point of view of imaging regional grid discretization,in the premise of ensuring the accuracy of migration imaging,to overcome the problem of over-sampling for high speed layer and under-sampling for low speed layer,this study puts forward the concept of multi-scale grid for RTM.The algorithm has a good flexibility which can image the geological model in the way of sparse and dense.Firstly,the multi-scale grid model is developed according to the velocity model,the small scale grid for the low speed area and large scale grid for high speed area are used.Secondly,the wave field value of each point is calculated based on the high order FDTD,especially the points in transition zone.Finally,the underground media is imaged based on the imaging condition.The experimental results show that under the condition of guaranteeing the accuracy of the same simulation order,the multi-scale RTM computational efficiency can be promoted by 25.05% average compared with the traditional method.
Key words:coalfield seismic exploration;multi-scale;high order FDTD;RTM;computational efficiency

移动阅读
张晓丹,刘贵忠,张志禹,等.多尺度高阶FDTD逆时偏移在煤田地震勘探中的应用[J].煤炭学报,2018,43(11):3169-3177.doi:10.13225/j.cnki.jccs.2018.0128
ZHANG Xiaodan,LIU Guizhong,ZHANG Zhiyu,et al.Application of multi-scale high order FDTD inverse time migration in the coalfield seismic exploration[J].Journal of China Coal Society,2018,43(11):3169-3177.doi:10.13225/j.cnki.jccs.2018.0128
收稿日期:2018-01-23
修回日期:2018-06-04
责任编辑:常明然
基金项目:国家自然科学基金青年基金资助项目(61401347);陕西省科技厅自然科学基础研究基金资助项目(2018JQ4016);陕西省教育厅自然科学专项基金资助项目(16JK1322)
作者简介:张晓丹(1981—),女,辽宁葫芦岛人,讲师,硕士生导师,博士。E-mail:zhangxiaodan@xpu.edu.cn
近年来,随着浅层构造简单条件的煤炭资源逐渐减少,煤田地震勘探难度日趋提高,面临的问题越来越难,主要表现为地层倾斜角大、煤层埋藏较深和介质纵横向速度变化非常剧烈等,故煤田地震勘探对偏移成像方法的计算效率与精度的要求也日益升高[1]。人们越来越关注如何同时提高偏移成像算法的效率和精度,一方面在提高算法成像精度的同时必然会使得算法的复杂度升高,导致计算量的增加,从而降低算法计算效率,另一方面在提升算法计算效率的同时,必然会牺牲偏移成像的精度,二者似乎是不可调和的矛盾体。
逆时偏移[2](Reverse Time Migration,RTM)基于精确的波动方程而不是对其近似,用时间外推来代替深度外推,因此它具有良好的精度,不受地下构造倾角和介质横向速度变化的限制,甚至对回转波也能正确成像[3-6],在采用有限差分方法进行RTM成像时,差分阶数的选择直接影响着成像精度和计算量,差分阶数选择越高成像越精准,但是由于其需要进行波场的正向递推与反向递推使得RTM的计算量也成倍增大[6-8],从而造成计算机耗时超长,而且保留全波场值对计算机的内存需求非常大[7-11],严重限制着RTM的实际应用。为了解决以上问题,前人做了相关研究,文献[12]对一阶弹性波方程采用变网格的方式进行波场的数值模拟,提高计算效率;文献[13-14]提出使用CPU和GPU并行策略提升RTM的计算效率,该方法从硬件方面入手,解决计算效率低的问题;文献[15]采用伪谱法解决空间导数的计算问题,从而提高算法计算效率;文献[16-17]采用高阶有限差分和边界条件相结合的方式,提高算法精度;文献[18]采用Kirchhoff积分法射线类偏移方法的高计算效率与逆时偏移反推相结合的方式;文献[19-21]提出了优选随机边界条件和吸收边界条件的有效边界存储策略,从而降低内存需求;文献[22]提出了1种基于云计算的逆时偏移计算方法,提升算法的计算效率;文献[23-24]分别从编码和低阶高效的角度出发,提高算法的计算效率;文献[25]提出将变网格方法应用于不同的观测数据中。
对RTM算法进行研究,力求能使得计算效率提升与成像精度二者达到一个平衡的状态。在对地下介质进行离散分析时,同样尺寸的网格在高速层区域往往会造成过采样,而同时采用稀疏网格离散化又会使得低速层和细薄夹层成像不清晰。设计一种在低速层采用小尺度网格,使其能够精细成像,而在高速层采用大尺度网格避免过采样,同时可以减少计算量和内存占有率,二者综合实现算法综合效率的提升,同时保证偏移成像结果的横向分辨率不受影响。实验结果验证了算法的有效性。
采用高阶有限差分的格式进行逆时偏移成像,以二维全波波动方程为例,可表示为
(1)
其中,U为波场函数u(x,z,t);v为介质速度v(x,z);S为震源函数s(x,z,t);x,z为空间坐标分量,x为水平方向;z为垂直方向;t为时间坐标分量。对于数学方程来说,如果u(x,z,t)为波动方程(1)的一个解,那么u(x,z,t-t0)同样为波动方程(1)的解,也就说在物理上任何事物只能随着时间递增变化,而在数学上时间却是可逆的。利用这个原理,逆时偏移成像才得以实现。将式(1)的x,z和t项分别进行Taylor级数展开,整理后可得空间2N阶时间2阶波动方程差分格式,如式(2)所示。
u(i,j,k-1)=2u(i,j,k)-u(i,j,k+1)+
2u(i,j,k)+u(i,j-n,k)]=2u(i,j,k)-
u(i,j,k+1)+Ax·Bx+Az·Bz
(2)
其中,Cn为差分系数,其值可由Taylor级数展开求得,
逆时偏移是波场正推(正演)和反推的卷积成像,波场的正推(正演)和反推互为逆过程。如图1所示为十八点格式的逆时偏移成像(时间二阶空间四阶)示意图,图中t-1时刻平面上红色五角星为待求网格点,该点需要t时刻平面上的17个网格点和t+1时刻平面上的1个网格点作为支撑,在t时刻平面上17个网格点的渐变颜色表示与待求点的关联程度,颜色越深关联程度越大,其由差分系数决定。

图1 十八点格式逆时偏移成像(时间二阶空间四阶)
Fig.1 RTM imaging of 18 points form(two order in time and four order in space)
对于横向速度变化不剧烈的地质模型,我们只需考虑其在纵向上的多尺度设计,使用小步长的网格对低速层进行剖分,使用较大步长网格对高速层进行剖分,这样,就可以在保证计算精度的前提下,有效的减少计算量,提高计算效率,在进行空间2N阶精度计算时,过渡带出现在以速度分界面为中心对称的共2N-1个网格点,在进行过渡带公式的推导时,发现过渡带公式的变化只与式(2)中Az,Bz项有关,而与其它项无关,故其它点的波场值均可按照常规方法计算。以时间二阶、空间十阶差分为例,上层为高速层采用稀疏网格,下层为低速层采用密集网格,而且稀疏网格间距为密集网格间距的2倍,在此条件下推导过渡带各点的波场公式,由以上分析可知,过渡带内波场点的计算关键在于t时刻时间切片上z方向11个点差分点数的确定。
图2是由高速层到低速层的过渡带各点波场递推示意图。其中第0列Z1和Z2之间红色形状表示过渡带,共9个点,其意味着如果待求网格节点位于t-1时间切片的红色形状位置时,将采用过渡带波场求解方法。低速层采用小步长网格,在图中用三角形表示,高速层采用2倍低速层步长进行采样,用圆形表示,六角形表示分界面。假设模型在x方向上各点速度一致或速度变化不大,用固定的步长Δx进行采样,故可用常规有限差分方法计算各点在x方向的差分点数,而在z方向上的网格步长是不连续的,故常规的有限差分方法并不适用,此处给出过渡带内各点的多尺度差分算法,红色形状表示待计算波场点。

图2 高速层到低速层过渡带各点波场递推
Fig.2 Wave field recursion of the points in transition zone from high-speed layer to low-speed layer
图2中第1列尚未进入过渡带,对应t-1时刻黑色点的波场值为
![]()
(3)
式中,an(n=0,1,…,5)为差分系数,在求导点的两侧差分点数一致。
图2中由第2列开始进入过渡带,因其求导点的两侧差分点数不再对称,所以差分系数也随之改变,红色圆点波场值Bz项如式(4)所示,其中bn(n=0,1,…,5)为差分系数。
![]()
(4)
过渡带在图2中从第2列开始由左向右给出,直至第11列离开过渡带,其中,左起第3列至第5列红色圆点的Bz项如式(5)~(7)所示,其中cn,dn,en(n=0,1,…,5)为差分系数。
![]()
(5)
![]()
(6)
![]()
(7)
第6列的红色六角形为分界线上的点,从该点开始Az项也发生变化,根据网格步长的变化Az项变为式(8),Bz项见式(9):

(8)
![]()
(9)
第7列至第10列红色三角形波场值的Az项均采用式(8)进行计算,而Bz项见式(10)~(13):
![]()
(10)
![]()
(11)
![]()
(12)
![]()
(13)
观察式(10)~(13)与式(4)~(7)发现,过渡带内各点的波场值求解公式关于边界点对称,这个规律可以很巧妙的用在编程代码的实现中,同时可以将差分点的变化作为新的函数引入Z方向的导数公式,得
(14)
其中,mk为差分系数,可由Taylor级数展开求得;n(k)为差分点数变化函数,十阶精度有限差分的n(k)取值见表1,而由低速层到高速层的过渡带差分格式可根据同理推导得出,X方向的多尺度RTM差分公式也可由此方法同理得到。
表1 十阶精度FDTD差分点数变化函数n(k)取值
Table 1 Value of n(k) at ten order FDTD difference point

多尺度差分方程的稳定性是保证多尺度RTM成像顺利进行的关键,常规网格差分格式的稳定性条件为
(15)
其中,m为稳定性条件,其值见表2。
表2 2N阶精度有限差分稳定性条件m值
Table 2 Value of mof 2N order FD stability condition

而多尺度偏移成像与传统偏移成像的不同在于网格的变化,以式(15)为基础将不同尺度网格融入上式,经分析可得,要满足稳定性条件只要使得不等式(15)左边的最大值小于m即可,故多尺度RTM的稳定性条件为
(16)
当空间和时间步长满足式(16)时,多尺度差分算法才可能稳定。
成像条件是决定偏移成像结果能否精准的重要条件之一。文献[26]指出成像条件是实现保幅偏移的关键,采用零延迟互相关成像条件,该条件有实现简易计算量小的优点,其原理是通过将各时刻的正时与逆时波场值进行卷积最终得到成像结果。逆时偏移成像的零延迟互相关成像条件可表示为
(17)
其中,Pr(x,z,t)为外推观测波场;Ps(x,z,t)为震源外推波场;积分核Pr(x,z,t)Ps(x,z,t)表示在t时刻对所在空间的全波场做1次成像运算,实现对同一成像网格点的多次成像,并且积分求和对成像噪声也具有很好的压制效果。
一般情况下使用普通PC机做逆时偏移成像是非常费时的,效率非常低,采用普通PC机进行模型的试算并论证方法的可行性和有效性。使用8G-Byte内存,处理器为Inter Core i5-7400的普通计算机进行模拟,震源采用30 Hz雷克子波,模拟精度均为时间二阶空间十阶。
该模型为层状结构,模型大小为100 m×200 m,第1层为1 200 m/s,第2层的速度为2 400 m/s,速度模型如图3所示。对于该速度模型,采用2种尺度网格进行设计,多尺度网格设计方法为:第1层采用dx=5 m,dz=2.5 m的Z方向小网格步长,第2层采用dx=5 m,dz=5 m的Z方向大网格步长,X方向网格大小不变,多尺度网格设计如图4所示,需要指出的是该算例是由低速层向高速层过渡,所用公式可由图2逆向递推获得。
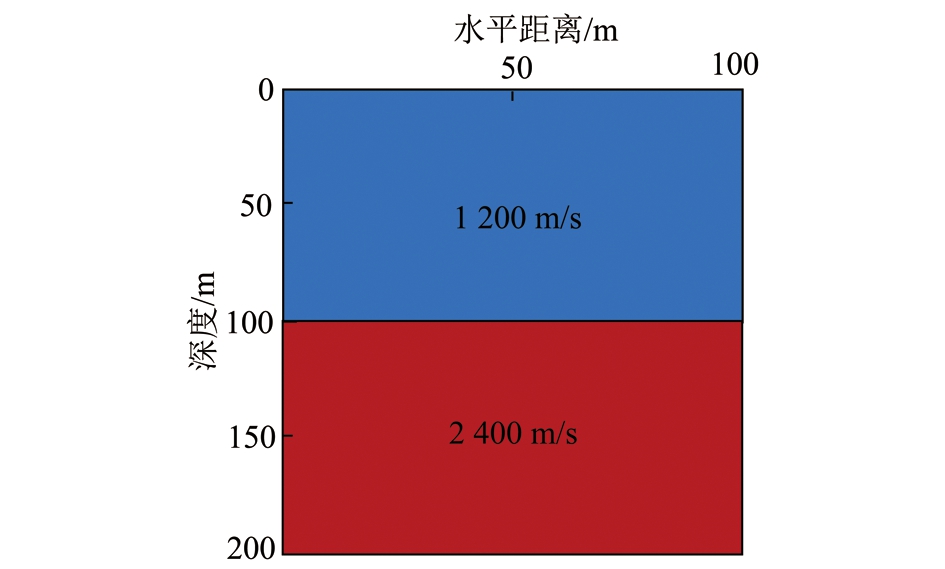
图3 速度模型
Fig.3 Velocity model

图4 多尺度网格设计
Fig.4 Multi-scale grid design
用该算例进行波场的正向模拟,炮点坐标设置为(50 m,75 m),时间采样间隔为0.5 ms,在t=30 ms时得到多尺度算法的波场快照如图5所示,图6为传统算法的波长快照,传统的模拟方法采用的是dx=5 m,dz=2.5 m的网格划分,由图中模拟结果的对比可见,多尺度方法在模拟结果的分辨率上与传统方法无异,能够较好的模拟波在地下介质中的传播,效果良好。
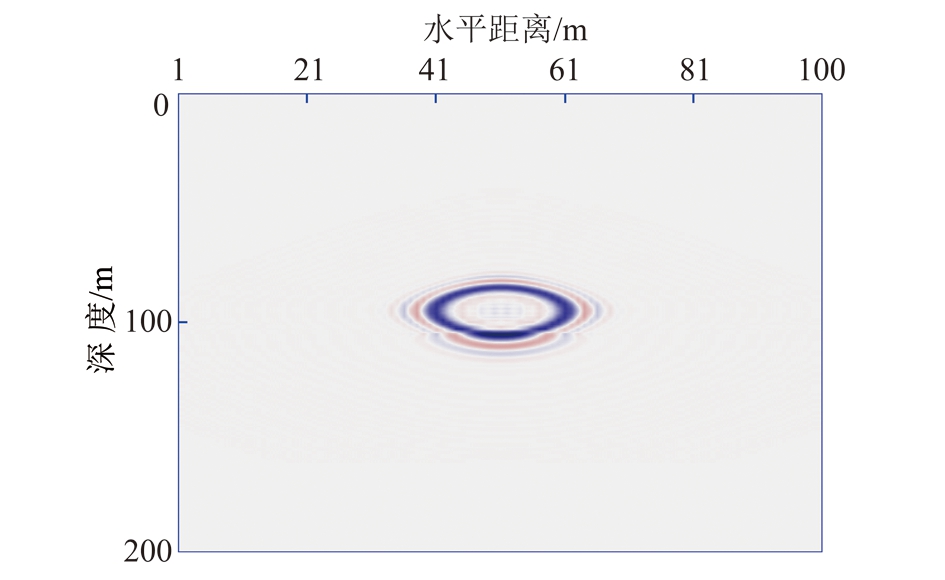
图5 t=30 ms时多尺度算法波场快照
Fig.5 Wave field snapshot at t=30 ms of multi-scale method

图6 t=30 ms时传统算法波场快照
Fig.6 Wave field snapshot at t=30 ms of traditional method
从综合计算效率的角度分析,在计算机机时与内存消耗量方面的对比见表2。由表2可见在层状速度模型中,在保证模拟精度的情况下,多尺度网格方法无论在计算时间和存储空间上都有所提高,算法的综合效率得到很好的提升,从省时的角度考虑对于该算例多尺度算法效率提升24.32%。
表2 多尺度方法与传统方法对比
Table 2 Comparisons of multi-scale method and traditional method

模型大小为100 m×200 m,第1层为1 200 m/s,第2层的速度为2 400 m/s,速度模型如图7所示,不同于2.1节的是该模型存在直角阶梯状,用以验证多尺度算法对大拐点是否适用。对于该速度模型,同样采用2种尺度网格进行设计,多尺度网格设计方法为:第1层采用dx=5 m,dz=2.5 m的Z方向小网格步长,第2层采用dx=5 m,dz=2.5 m的Z方向大网格步长,X方向网格大小不变,多尺度网格设计如图8所示。

图7 阶梯状速度模型
Fig.7 Velocity model of ladder shaped
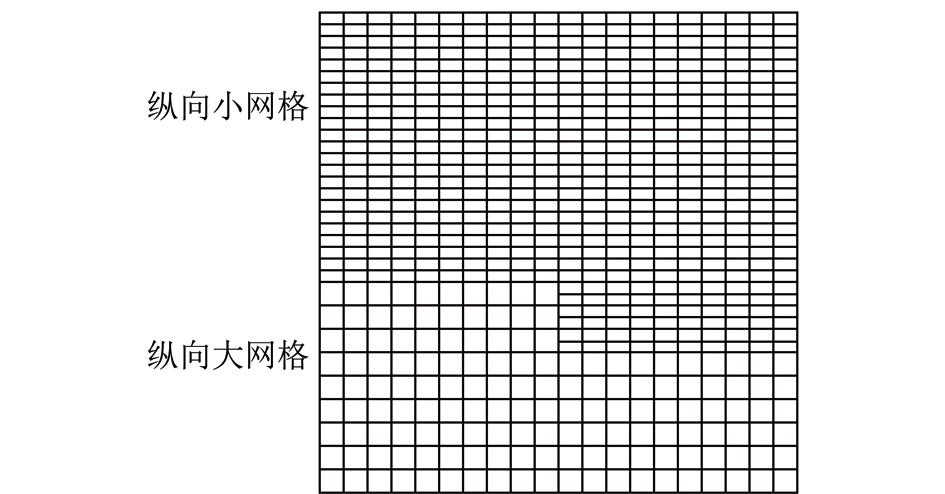
图8 多尺度网格设计
Fig.8 Multi-scale grid design
用该算例进行波场的正向模拟,炮点坐标设置为(50 m,75 m),时间采样间隔为0.5 ms,在t=50 ms时得到多尺度算法的波场快照如图9所示,图10为传统算法的波长快照,传统的模拟方法采用的是dx=5 m,dz=2.5 m的网格划分,由图中模拟结果的对比可见,多尺度方法在模拟结果的分辨率上与传统方法无异,在遇到阶梯状大拐点的情况下能够较好的模拟波在地下介质中的传播,效果良好。

图9 t=50 ms时多尺度算法波场快照
Fig.9 Wave field snapshot at t=50 ms of multi-scale method

图10 t=50 ms时传统算法波场快照
Fig.10 Wave field snapshot at t=50 ms of traditional method
从综合计算效率的角度分析,在计算机机时与内存消耗量方面的对比见表3。由表3可见在层状速度模型中,在保证模拟精度的情况下,多尺度网格方法无论在计算时间和存储空间上都有所提高,算法的综合效率得到很好的提升,从省时的角度考虑对于该算例多尺度算法效率提升15%,由该算例和层状算例对比可见效率的提升并非是固定值,此例的提升效率反而下降,分析其原因是由于速度模型的多尺度设计,高速层所占区域相比于层状模型较少,导致大网格的划分区域变小,故计算量降低的少,故该算例的效率提升没有2.1节高。
表3 多尺度方法与传统方法对比
Table 3 Comparisons of multi-scale method and traditional method

Salt模型汇集了多种高难度的偏移成像难题:大倾角,多拐点,速度变化剧烈等。图11为Salt的速度模型,由图中可见该区域的速度变化剧烈,存在大倾角,倾角度数逼近90°,盐体的存在导致小间隙多拐点的出现,这种小间隙多拐点的处理对偏移成像是难点,并对盐体下部的介质成像同时也存在挑战。
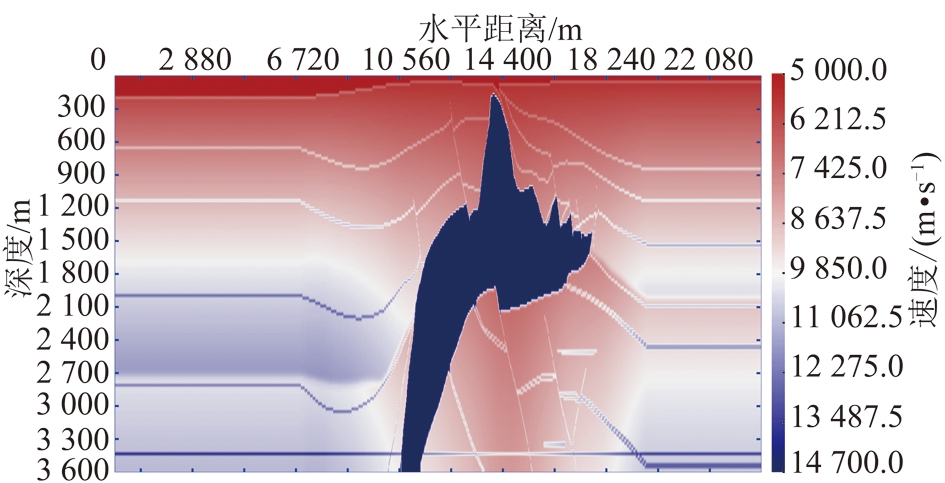
图11 Salt速度模型
Fig.11 Velocity model of Salt
分别采用3种传统模型与本文的多尺度模型进行对比,采用如图12所示的多尺度划分,其中尺度一为小尺度参数(dx=12 m,dz=12 m),尺度二为中尺度参数(dx=24 m,dz=24 m),尺度三为大尺度参数(dx=48 m,dz=48 m)。传统的模型网格化采用的是固定尺度对整个模型进行偏移成像,原始速度模型采用的小尺度划分,其RTM成像的结果如图13所示,而通过对速度模型的观察发现蓝色区域速度较高故可以采用尺度较大的网格进行划分,可以起到缩短成像时间的作用,故采用中尺度对速度模型进行划分,其RTM成像的结果如图14所示,由图13和14对比可见图14中红色椭圆盐体边缘大角度成像分辨率低,而且盐体下的细小断层也存在同样的问题,但是在盐体内部边缘成像清晰,故进一步增大步长,采用大尺度划分Salt模型,其RTM成像结果如图15所示。
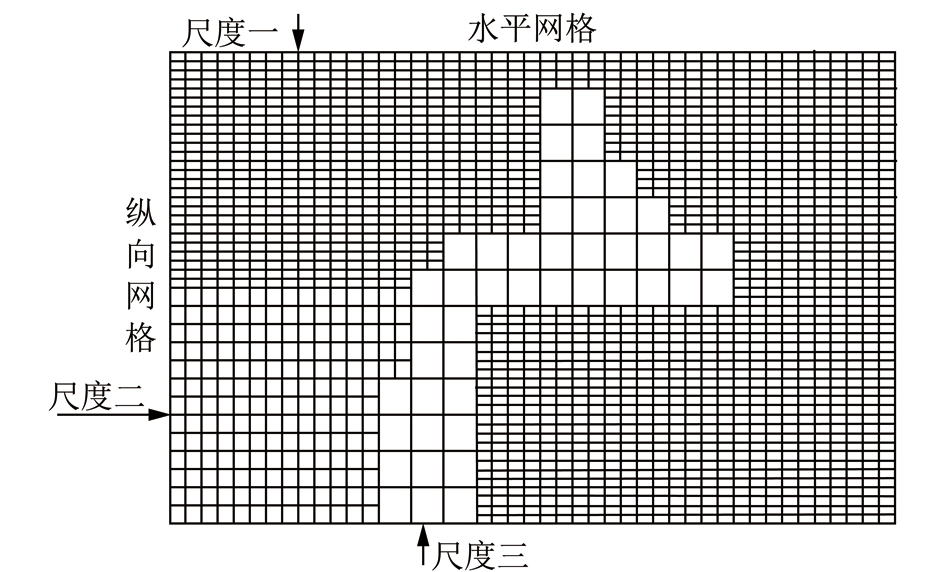
图12 Salt模型多尺度划分示意
Fig.12 Multi-scale partition of Salt model
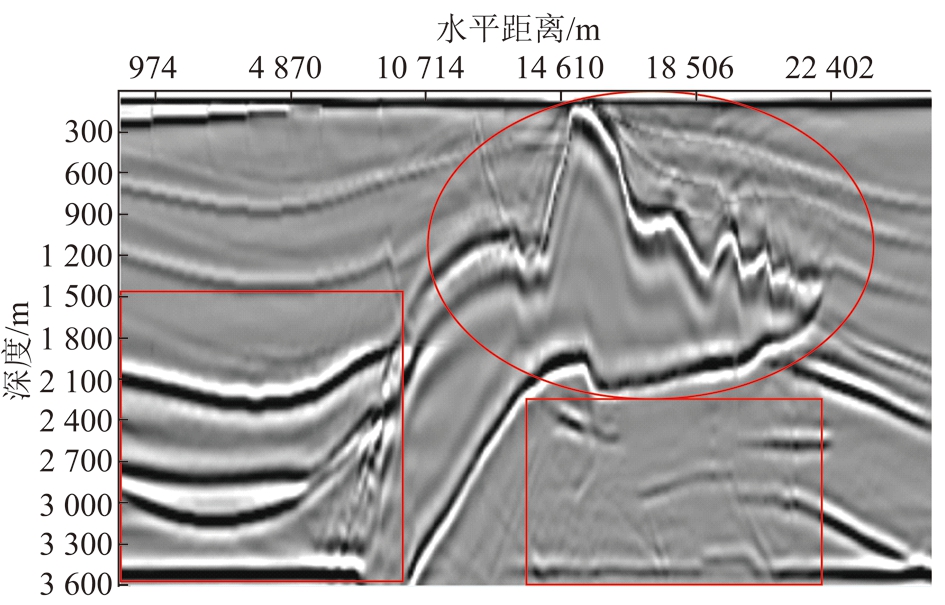
图13 小尺度传统RTM成像结果
Fig.13 Traditional RTM imaging result of small scale
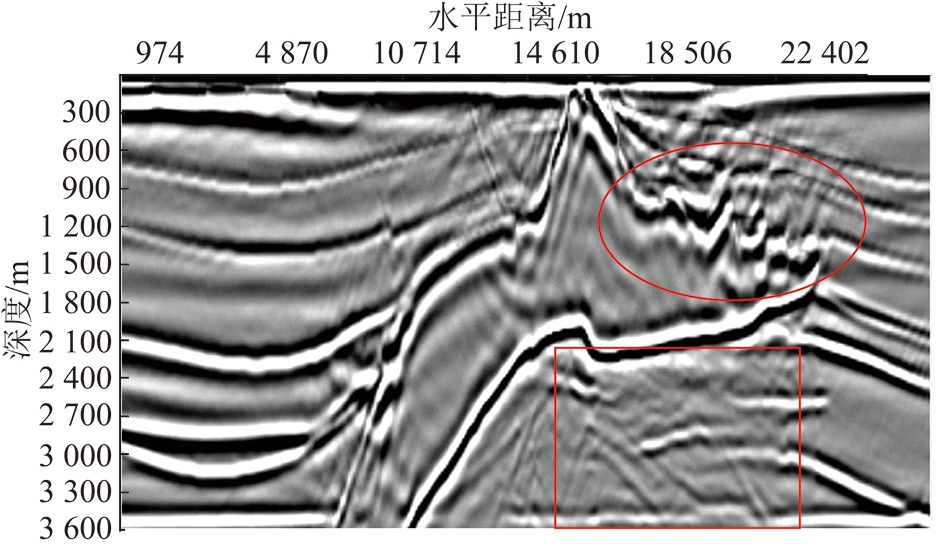
图14 中尺度传统RTM成像结果
Fig.14 Traditional RTM imaging result of middle scale
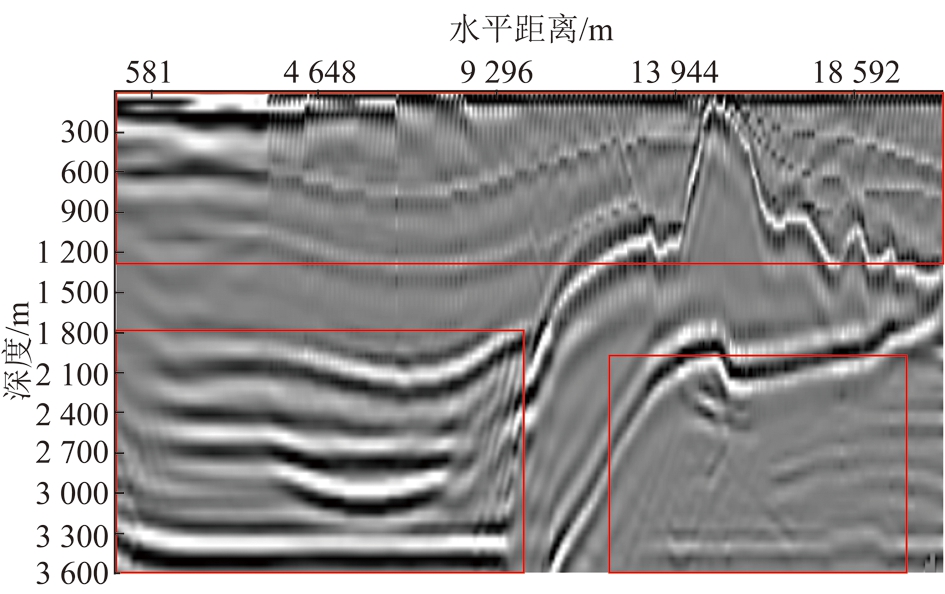
图15 大尺度传统RTM成像结果
Fig.15 Traditional RTM imaging result of big scale
图12表示的是尺度划分示意图,只显示尺度划分区域,并未显示该区域网格真实数量,另外,需要指出的是采用多尺度RTM方法时盐体边缘区域依然采用的是小尺度网格,用以保证边缘大倾斜角的成像分辨率。在进行多尺度划分时尽量保证大尺度是小尺度的偶数倍,其倍数的选择依据二者速度的大小,一般情况下速度成偶数倍关系时,尺度选择同样采用偶数倍关系,而当速度非偶数倍关系时选择最小的偶数倍关系,该例采用3种尺度,其中尺度一(小尺度)和尺度二(中尺度)区域的速度几乎是2倍的关系,故这两个区域采用2倍的尺度划分,而深蓝色区域的速度为14 700 m/s,而红色低速区域速度为5 000 m/s,二者是几乎是3倍的关系,但此处采用4倍的尺度关系三(大尺度),原因在于如果取3倍的尺度关系,会使得差分点无法取整,故采用4倍的尺度关系。
对比图13~15可见随着尺度的变大成像清晰度越来越差,多尺度RTM成像结果如图16所示,可见其成像清晰度均优于中尺度和大尺度方法,而且在大尺度情况下出现了低速区产生了较严重的频散现象,而多尺度RTM方法恰好能够避免低速区的频散现象,而同时又可对高速区进行大尺度划分,从而提高RTM算法计算效率。图13~16中红色椭圆区域对比成像分辨率清晰,说明在盐体进行4倍尺度的正演与逆时反推时能够保证成像分辨,红色方框内是进行2倍尺度的处理,该部分成像结果对比良好,下面从计算机机时和内存消耗方面进行分析。

图16 多尺度RTM成像结果
Fig.16 Multi-scale RTM imaging result
表5为多尺度逆时偏移成像与传统逆时偏移成像算法在计算机机时和内存消耗方面的对比,表中s表示秒,h表示小时,MB表示兆比特,GB表示千兆比特,由表5可见无论在计算机机时还是内存消耗量方面多尺度RTM都要比传统小网格RTM有所提升,提升效率的高低主要由节省的计算量决定,而对于传统大尺度网格和中尺度网格RTM虽然在计算机机时和内存消耗量方面多尺度方法都稍弱一些,但是在成像分辨率方面其优势较大,综合考虑以上2点本文的多尺度RTM能够保证计算效率和成像精度二者同时提升。
表5 多尺度RTM与传统RTM的对比
Table 5 Comparisons of multi-scale method and traditional method

(1)通过算例验证了多尺度逆时偏移成像算法在不降低成像精度的情况下,能够有效提高算法的综合计算效率,综合文中算例计算效率平均可提升25.05%,是一种行之有效的提升计算效率的方法。
(2)深层高速区采用大步长网格可降低RTM整体计算量,提升RTM计算效率。
(3)针对深层的低速夹层采用小网格,细化该部分区域,使得RTM成像结果更精准。
(4)无需在过渡带进行插值,有效地避免了由插值引起的误差累积.
(5)不足点在于采用多尺度方式进行变化时会出现轻微的数值频散现象,分析原因是由于网格间隔的变化、层速度和采样时间三者的协同关系,但并不影响偏移成像结果的分析。
综上所述,多尺度逆时偏移成像具有高效精准的特性,有利于逆时偏移成像技术在煤田地质勘探中的应用,通过实验验证该算法是有效和可靠的。
参考文献:
[1] 李振春,李雪松,肖建恩,等.基于互相关成像条件的保幅高斯束逆时偏移[J].物探化探计算技术,2017,39(3):354-358.
LI Zhenchun,LI Xuesong,XIAO Jianen,et al.Amplitude-preserved reverse time migration with Gaussian beam based on crosscorrelation imaging conditions[J].Computing Techniques for Geophysical and Geochemical Exploration,2017,39(3):354-358.
[2] BAYSAL E,KOSLOFF D D,SHERWOOD J W C.Reverse time migration[J].Geophysics,1983,48(11):1514-1524.
[3] GUAN H,DUSSAUD E,DENEL B,et al.Techniques for an efficient implementation of RTM in TTI media[A].USA:SEG 81st Annual International Meeting[C].2011:3393-3397.
[4] DAI W,FOWLER P,SCHUSTER G T.Multisource least-squares reverse-time migration[J].Geophysical Prospecting,2012,60(4):681-695.
[5] 文虎,张铎,郑学召,等.基于FDTD的电磁波在煤中传播特性[J].煤炭学报,2017,42(11):2959-2967.
WEN Hu,ZHANG Duo,ZHENG Xuezhao,et al.Propagation characteristics of electromagnetic wave based on FDTD in coal[J].Journal of China Coal Society,2017,42(11):2959-2967.
[6] ZHANG Y,DUANG L,XIE Y.A stable and practical implementation of least-squares reverse time migration[A].Houston:SEG 83rd Annual International Meeting[C].2013:3716-3720.
[7] LIU Y,SYMES W W,LI Z.Multisource least-squares extended reverse-time migration with preconditioning guided gradient method[C].Houston:SEG 83rd Annual International Meeting,2013:1251.
[8] DAVID C Del Rey Fernandez,JASON E Hicken,DAVID W Zingg.Review of summation-by-parts operators with simultaneous approximation terms for the numerical solution of partial differential equations[J].Computers & Fluids,2014,95: 171-196.
[9] SJÖGREEN B.High order finite difference and finite volume methods for advection on the sphere[J].Journal of Scientific Computing,2012,51(3):703-732.
[10] SJÖGREEN B,PETERSSON N A.A fourth order accurate finite difference scheme for the elastic wave equation in second order formulation[J].Journal of Scientific Computing,2012,52(1):17-48.
[11] RAO Y,WANG Y H.Seismic waveform simulation with pseudo-orthogonal grids for irregular topographic models[J].Geophysical Journal International,2013.194(3):1778-1788.
[12] LI Zhenchun,ZHANG Hui,ZHANG Hua.Variable-grid high-order finite-difference numeric simulation of first-order elastic wave equation[J].Oil Geophysical Prospecting,2008,43(6):711-716.
[13] 张志禹,侯文婷,苗永康.步长自适应的有限差分复杂地表波场数值模拟[J].地球物理学进展,2017,32(3):1321-1330.
ZHANG Zhiyu,HOU Wenting,MIAO Yongkang.Seismic wave simulation method based on variable grid step[J].Progress in Geophysics,2017,32(3):1321-1330.
[14] 李博,刘红伟,刘国峰,等.地震叠前逆时偏移算法的CPU/GPU实施对策[J].地球物理学报,2010,53(12):2938-2943.
LI Bo,LIU Hongwei,LIU Guofeng,et al.Computational strategy of seismic pre-stack reverse time migration on CPU/GPU[J].Chinese Journal of Geophysics,2010,53(12):2938-2943.
[15] CAI Zhicheng,GU Hanming,CHENG Jingwang,et al.Parallel large-scale variable grid 3D seismic wave modeling[J].Oil Geophysical Prospecting,2017,52(3):468-476.
[16] 王伟国,熊水金,徐华宁,等.TTI介质各向异性伪谱法逆时偏移[J].石油地球物理勘探,2012,47(4):566-572,682,513.
WANG Weiguo,XIONG Shuijin,XU Huaning,et al.TTI media anisotropic pseudo-spectral method inverse time migration[J].Petroleum Geophysical Exploration,2012,47(4):566-572,682,513.
[17] KOZDON J E,DUNHAM E M,NORDSTROM J.Simulation of dynamic earthquake ruptures in complex geometries using high-order finite difference methods[J].Journal of Scientific Computing,2013,55(1):92-124.
[18] SUN Linjie,LIU Chuncheng,ZHANG Shixin.A variable grid finite-difference scheme with PML boundary condition in elastic wave of porous media[J].Geophysical Prospecting for Petroleum,2015,54(6):652-664.
[19] 黄建平,张晴,张凯,等.格林函数高斯束逆时偏移[J].石油地球物理勘探,2014,49(1):101-106,303.
HUANG Jianping,ZHANG Qing,ZHANG Kai,et al.Green function gaussian beam inverse time deviation[J].Petroleum Geophysical Exploration,2014,49(1):101-106,303.
[20] 王保利,高静怀,陈文超,等.地震叠前逆时偏移的有效边界存储策略[J].地球物理学报,2012,55(7):2412-2421.
WANG Baoli,GAO Jinghuai,CHENG Wenchao,et al.Efficient boundary storages straregies for seismic inverse time migration[J].Chinese Journal of Geophysics,2012,55(7):2412-2421.
[21] 赵海霞,高静怀,马逸尘.弥散黏滞性波动方程的吸收边界算法[J].西安交通大学学报,2012,46(4):112-118.
ZHAO Haixia,GAO Jinghuai,MA Yichen.An absorbing boundary algorithm for diffusive-viscous wave equation[J].Journal of Xi’an Jiaotong University,2012,46(4):112-118.
[22] 高新成.基于云计算的逆时偏移数据处理方法研究[D].大庆:东北石油大学,2016.
GAO Xincheng.Research on the method of inverse time migration data processing based on cloud computing[D].Daqing:Northeast Petroleum University,2016.
[23] 李娜.基于Huber范数的多震源最小二乘逆时偏移[J].石油地球物理勘探,2017,52(5):941-947,878.
LI Na.Multi-source least-squares inverse time migration based on Huber norm[J].Petroleum Geophysical Exploration,2017,52(5):941-947,878.
[24] WANG Ying,ZHOU Hui,YUAN Sanyi,et al.A fourth order accuracy summation-by-parts finite difference scheme for acoustic reverse time migration in boundary-conforming grids[J].Journal of Applied Geophysics,2017,136:498-512.
[25] SUN Xiaodong,LI Zhenchun,JIA Yanrui.Variable-grid reverse-time migration of different seismic survey data[J].Applied Geophysics,2017,14(4):517-522,621.
[26] 王娟,李振春,陶丽.逆时偏移成像条件研究[J].地球物理学进展,2012,27(3):1173-1182.
WANG Juan,LI Zhenchun,TAO Li.The research on imaging condition of reverse time migration[J].Progress in Geophysics,2012,27(3):1173-1182.