神东煤田埋深较浅,地质条件简单,可开采煤层 4~5 层,上组可采煤层房式采空区中煤柱主要由早期小煤矿房式采煤和后期旺采方法形成,不同形状、尺寸煤柱控制顶板及地表沉降,仅鄂尔多斯境内的房式采空区面积约 307.61 km2 。其中,存在房式采空区的大型井田有伊泰集团纳林庙、凯达、宏景塔[1]。神东矿区的寸草塔二矿、上湾煤矿、大柳塔煤矿、哈拉沟煤矿、榆家梁煤矿、寸草塔一矿、柳塔煤矿、乌兰木伦煤矿、补连塔煤矿、石圪台煤矿、保德煤矿等11座煤矿[2]。房采采空区主要存在资源安全、井下安全生产(压架事故频繁)、地表建(构)筑物安全、生态和社会安全等隐患[3-4]。采空区稳定结构为“底板—煤柱—顶板”,煤柱稳定性决定采空区整体结构稳定状态[5]。煤层房式开采后,煤柱上方应力重新分布,煤柱群的稳定性直接影响下方长壁工作面推进过上方煤柱时顶板压力大小,应力二次分布后煤柱上方垂直应力小于煤体强度极限时,煤柱群整体稳定,反之,煤柱失稳。稳定的房式煤柱中心弹性核区为应力集中区域,工作面出煤柱时顶板压力大,易发生切顶压架事故。因此,评价房式采空区中煤柱稳定性以确保下组煤层安全开采成为国内外学者研究的重点内容。
影响房式煤柱稳定性因素众多[6-7],从不同角度预测判断煤柱稳定性方法也很多,其中,突变理论在煤柱失稳预测应用较早,尖点突变模型研究已提供煤柱失稳路径,判别式等对单一煤柱适用性较强[8-10]。蒙特卡洛法、逻辑回归法、半定量、概率逼近、模糊集合等数理统计方法在房式煤柱稳定性评估上应用广泛[11-18],此类方法对影响煤柱稳定的因素和事件考虑比较充分,但煤柱及采空区顶板应力状态变化等因素未参与计算。由于房式采空区中煤柱数量多,煤柱间距小,相邻煤柱之间稳定性互相影响。因此,断开煤柱群之间相互影响关系仅考虑某一个煤柱稳定性使得煤柱群稳性评估不够准确。重整化群方法通过系统内部基本组成单元进行自相似变化,从而描述宏观稳定性状态,结合威布尔失稳概率分布模型,计算系统稳定临界条件,分析房式采空区中煤柱群稳定性。本文利用概率统计及逻辑回归方法充分考虑煤柱分布方式,煤柱尺寸、强度,煤柱上覆载荷及煤柱间应力转移等因素对煤柱群系统稳定性影响。
1 煤柱失稳临界条件研究
1.1 房式煤柱群
房式煤柱群分布如图1所示,房式采空区已研究工作中煤柱分布方式多为矩阵元素排列式分布[19-21]。神东煤田房式开采方法相关文献资料及实地调研现场揭露煤柱分布形式为“品”型对称分布[22-24],房式煤柱空间位置关系及赋存状态如图1所示,图1中上部为房式煤柱分布规律,图1下部图形采用局部放大的方法的描述了P32煤柱的立体结构,煤柱水平截面形状近似为正方形。图中w1,w2为煤柱截面边长,b1,b2为煤柱间距,h为煤柱高度(采高)。

图1 房采煤柱群分布规律
Fig.1 Distribution law of room mining residual pillar system

图2 不同煤房宽度对应压力拱拱角分类[25-26]
Fig.2 Schematic of different room widths corresponding to abutment angle[25-26]
如图2所示,基于采空区顶板塑性区拱角的煤柱上覆载荷[27]:
σaps=
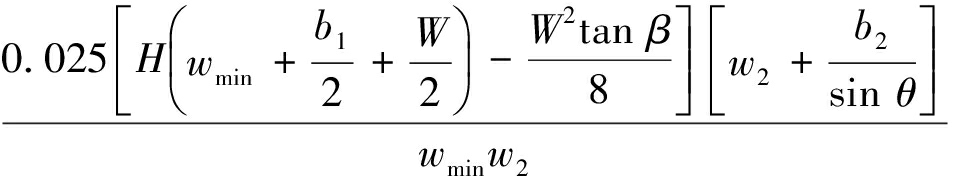
(1)
wmin=w1sin θ
式中,w1,w2为煤柱截面边长;b1,b2为煤柱间距;β为采空区顶板冒落拱切线与竖直方向夹角;θ为煤柱边界线间内错角(θ<90°);W为房采工作面宽度。
考虑采空区冒落拱对煤柱上覆载荷影响时[26,28]:
(2)
式中,L为煤柱间载荷传递大小(Ls 或 Lss);γ为覆岩容重;H为覆岩厚度。
(3)
如图3所示,失稳煤柱上方载荷传递最大距离
(4)
(5)

图3 垂直应力在煤柱上方分布规律[29]
Fig.3 Transfer law of load on pillar[29]
煤柱强度[30]可表示为
(6)
式中,h为煤柱高度,m。
定义煤柱单元体失稳概率P0:
(7)
1.2 基于重整化群方法的煤柱群失稳理论
1.2.1 一维重整化煤柱群模型
房式采空区由煤柱支撑起稳定性,采空区中任一煤柱失稳均会引起其它煤柱上覆载荷重新分布,重整化群方法表明此煤柱失稳可导致整个采空区稳定状态改变,垂直于地层与工作面做切面,建立房式煤柱群元胞模型,一维Ising模型如图4所示,一级元胞由煤柱和其两侧各一半采空区构成。

图4 煤柱群一级元胞简图
Fig.4 Schematic of one-dimensional pillar system
结合煤柱设计原理、煤柱上覆载荷分布、煤柱内弹、塑性区域分布[31-33]及重整化群方法,将煤柱分为3个基元,建立一级元胞中煤柱失稳概率模型,一维重整化煤柱群上覆垂直载荷可表示为
(8)
煤柱稳定状态分为4类,如图5所示。

图5 煤柱群一级元胞稳定状态分类
Fig.5 Stable state classification of the level Ⅰ cell pillar system
煤柱单元失稳概率为P0,图5(a)为完整煤柱,失稳概率为0;图5(b)为煤柱2个单元为塑性区,1个为弹性区情形,其发生失稳概率为3P0[(1-P0)Pab]2;图5(c)为煤柱1个单元为塑性区,2个为弹性区情形,其发生失稳概率为![]() 图5(d)为煤柱完全失稳,概率为
图5(d)为煤柱完全失稳,概率为![]()
一级元胞失稳破坏概率:
(9)
Pab为煤柱外侧单元损伤后应力向内部邻近单元的传播条件概率,可表示为
(10)
式中,Pa为煤柱外部单元处于塑性状态前其相邻内部单元处于塑性状态的概率,煤柱承载为σups;Pb为煤柱外部单元处于塑性状态后其相邻内部单元处于塑性状态失稳的概率,此时煤柱承受载荷为σi=σaps+σa。
内局部故障或失效引起的系统失效相关问题均服从Weibull分布,煤柱失稳统计概率密度函数(PDF)f(σi)可表达为Weibull函数分布形式:
(11)
式中,mi为关于基元强度的相似性的参数;σi为第i个元胞上覆载荷;σps为煤柱强度极限。
累计密度函数(CDF)为
(12)
1-(1-P0)mi-1
(13)
可靠度函数为
(14)
σi=0时,R(σi)=exp(0)=1,可靠度为100%,失稳率为0;σi=σps时,R(σi)=exp(-1)=36.8%,可靠度为36.8%,其发生失稳率为63.2%。
mi=3时一级元胞不动点方程表示为[10]
3x(1-x)2[1-(1-x)2]2+3x2(1-x)
[1-(1-x)4]+x3=x
(15)
不动点共3个:0,0.315,1,考虑不动点实际意义忽略0,1两个不动点,结合可靠度分析得:一级元胞失稳概率为31.5%,即临界指数为31.5%,36.8%≥P0≥31.5%时,一级元胞向失稳趋势演化,P0≥36.8%时煤柱整体处于完全塑性状态。
1.2.2 二维重整化煤柱群模型
由“品”字形煤柱分布特征可将二维重整化煤柱群模型表示为图6所示,一级,二级与三级元胞如图6中标注所示。

图6 二维重整化煤柱群平面模型
Fig.6 Two-dimensional renormalized pillar system
二级元胞中心煤柱破坏后,四周煤柱上覆载荷可描述为
σi=σaps+σa=(1+k)σaps
(16)
由威布尔失稳密度分布函数得二级元胞外围煤柱失稳概率
式中,k为垂直应力传递系数;mi为煤柱基元强度相似性参数。
二级元胞煤柱群失稳概率为
P2=7[1-(1-p0)2]6(1-p0)6p0+
21[1-(1-p0)2]5(1-p0)5p02+35[1-
(1-p0)2]4(1-p0)4p03+
35[1-(1-p0)2]3(1-p0)3p04+
21[1-(1-p0)2]2(1-p0)2p05+
7[1-(1-p0)2](1-p0)p06+p07
(18)
求解其不动点方程得到有实际意义的解为![]()
N级元胞煤柱群失稳概率为
n=6(N-1)+1;N=1,2,3,…
(19)
由上文分析可知,影响房式采空区稳定性的因素众多,包括埋深、煤体强度、煤柱尺寸等,采用控制变量的方法分析各变量对煤柱稳定性的影响,以埋深H为例。
将式(6),(8)代入式(7)得埋深H对一级、二级煤柱元胞稳定性影响描述如下:
(20)
![]()
(21)
绘制式(20),(21)如图7所示,一级元胞失稳的临界埋深为110.4 m,埋深大于临界深度,一级元胞整体处于塑性状态;埋深为94.5~110.4 m时一级煤柱元胞向失稳趋势演化;埋深小于94.5 m时一级元胞整体稳定。二级元胞煤柱群失稳的临界深度为173.4 m。

图7 埋深对煤柱稳定性的影响
Fig.7 Influence of buried depth on the stability of coal pillars
2 实例分析
2.1 石圪台煤矿房式采空区煤柱稳定性分析
石圪台煤矿位于内蒙古自治区鄂尔多斯市伊金霍洛旗境内,神东煤田的北部,井田内主采煤层3-1-1号、3-1-2号煤层分别采用房式开采方法与长壁综采方法,上、下煤层巷道布置方式及相对位置关系如图8所示。
(1)一维重整化煤柱群元胞稳定性
表1中参数带入式(6),(7),(8)得
σaps=2.6,σps=10.37,P0=0.251
式(10)不动点解![]() 对比得
对比得
因此,一维重整化煤柱群元胞处于稳定状态,无整体失稳的可能性。
(2)二维重整化煤柱群元胞稳定性
表1中参数带入式(1),(6),(7)计算得
σaps=5.19,σps=10.37,P0=0.548

图8 上、下煤层巷道布置及房式煤柱分布形式
Fig.8 Layout of roadways in upper and lower coal seams and distribution pattern of room mining residual pillar
表1 石圪台煤矿房式采空区参数[34]
Table 1 Dimension of room mining goaf in Shigetai Mine[34]

式(10)不动点解![]() 对比得
对比得
因此,二维重整化煤柱群元胞处于稳定状态,无整体失稳的可能性。
2.2 数值模拟
结合石圪台煤矿开采现状及表2中煤岩埋深及力学参数等条件,利用FLAC3D数值模拟软件建立煤柱群数值计算模型如图9(a),(b)所示。模型大小为200 m×200 m×80 m,模型上表面自由,下表面x,y,z三个方向固定,固定其他面法向方向,侧压系数为1.2。图9(a)模型上表面未到达地表,因此,施加大小1.1 MPa压应力边界条件,数值模拟结果如图9所示。
表2 岩层厚度分布及岩石力学参数
Table 2 Thickness of rock strata and rock mechanical parameters


图9 煤柱群稳定性数值模拟
Fig.9 Numerical simulation of stability of pillar system
图9(a)所示60 m×60 m×18 m范围内二维重整化煤柱群二级元胞数值计算过程中垂直应力及塑性区分布情况,随计算步数增加煤柱塑性区范围由两侧向中间发育,计算平衡后,煤柱中均存在弹性区。因此,二级元胞煤柱处于稳定状态。图9(b)所示200 m×200 m范围内煤柱群稳定性计算模型平衡后的垂直应力及塑性区分布情况,煤柱四周边界存在塑性区域,煤柱群整体处于稳定状态。
2.3 现场实测
为研究房式采空区及煤柱稳定状态,验证上文理论预测准确性,如图7蓝色线框区域1434工作面,1435工作面房式工作面具有埋深较浅,靠近井田边界等有利特征,选取其进行表土层剥离揭露实验,同时可采用露天开采回收煤柱,实验揭露了房式采空区中煤柱分布形式、参数及煤柱稳定性状态如图10所示。

图10 表土层剥离实验揭露房式煤柱稳定性
Fig.10 Epipedon stripping experiment exposes the stability of the room mining residual pillar
剥离表土层后揭露1434,1435工作面如图9所示,房式煤柱整体呈“品”字形分布,煤柱尺寸基本相同,煤柱四周存在少量煤块脱落现象但煤柱整体处于稳定状态,房式煤柱群及采空区群均处于稳定状态。表明本文提出的煤柱群稳定性判断模型以及数值模拟结果可靠性强,可以为后续房式采空区下开采遗留煤柱稳定性判断提供理论指导。
3 结 论
(1)基于房式煤柱上覆载荷及煤柱强度计算方法定义了煤柱单元失稳概率,结合重整化群理论将房式采空区中煤柱群分为一维、二维重整化煤柱群模型,将煤柱失稳概率密度函数(PDF)表示为威布尔函数分布形式,计算得出重整化煤柱群元胞失稳概率,利用不动点方程理论确定元胞失稳不动点方程及其有效解,此解作为判断煤柱失稳概率的临界值![]()
(2)结合石圪台煤矿房式开采技术参数及地质资料分别计算3-1-1号煤层房式采空区中一维、二维重整化煤柱群中元胞失稳概率P0,对比煤柱失稳临界值得出石圪台煤矿3-1-1号煤层采空区中煤柱群无整体失稳可能性。利用数值模拟方法同样得出了煤柱群整体处于稳定状态的结果。
(3)选取井田边界处埋深较浅的1434号,1435号房式采空区进行地表剥离,揭示了采空区内煤柱群稳定性,验证了重整化煤柱群失稳概率理论计算的正确性,同时为有效预测相邻采区、井田内房式采空区中煤柱群分布规律、尺寸参数、稳定性提供工程及理论借鉴。
参考文献(References):
[1] 张永爱.房式采空区遗留煤炭资源回收及生态重建[J].煤矿安全,2014,45(2):197-199.
ZHANG Yongai.Residual coal resource recovery and ecological recon-struction for room mining goaf[J].Safety in Coal Mines,2014,45(2):197-199.
[2] 张俊英,李文,杨俊哲,等.神东矿区房采采空区安全隐患评估与治理技术[J].煤炭科学技术,2014(10):14-19.
ZHANG Junying,LI Wen,YANG Junzhe,et al.Research on hazard assessment and control technology of room and pillar mining method goaf in shendong mining area[J].Coal Science & Technology,2014(10):14-19.
[3] 李文,李健.浅埋煤层房采采空区隐患分析与治理技术[J].煤矿安全,2014,45(1):64-66.
LI Wen,LI Jian.Goafs Hazard analysis and control technology of room mining in shallow coal seam[J].Safety in Coal Mines,2014,45(1):64-66.
[4] 许家林,朱卫兵,鞠金峰.浅埋煤层开采压架类型[J].煤炭学报,2014,39(8):1625-1634.
XU Jialin,ZHU Weibing,JU Jinfeng.Supports crushing types in the longwall mining of shallow seams[J].Journal of China Coal Society,2014,39(8):1625-1634.
[5] 张勇,潘岳.弹性地基条件下狭窄煤柱岩爆的突变理论分析[J].岩土力学,2007,28(7):1469-1476.
ZHANG Yong,PAN Yue.Analysis of rockburst in narrow coal pillar by fold catastrophe theory on the condition of elastic foundation[J].Rock & Soil Mechanics,2007,28(7):1469-1476.
[6] 潘岳,张孝伍.狭窄煤柱岩爆的突变理论分析[J].岩石力学与工程学报,2004,23(11):1797-1803.
PAN Yue,ZHANG Xiaowu.Catastrophe theory analysis on rockburst in narrow coal pillar[J].Chinese Journal of Rock Mechanics & Engineering,2004,23(11):1797-1803.
[7] 江文武,徐国元,马长年.基于尖点突变理论的矿房间矿柱的稳定性分析[J].金属矿山,2007(9):39-41.
JIANG Wenwu,XU Guoyuan,MA Changnian.Stability analysis of intermittent pillar between stope rooms based on cusp catastrophe theory[J].Metal Mine,2007(9):39-41.
[8] 张淑坤,张向东,孙琦,等.基于重整化群理论的采空区煤柱群临界失稳概率研究[J].中国安全生产科学技术,2016,12(5):104-108.
ZHANG Shukun,ZHANG Xiangdong,SUN Qi,et al.Study on critical instability probability of coal pillar group in goaf based on renormalization group theory[J].Journal of Safety Science & Technology,2016,12(5):104-108.
[9] 周子龙,李夕兵,赵国彦.民窿空区群级联失稳评价[J].自然灾害学报,2007,16(5):91-95.
ZHOU Zilong,LI Xibing,ZHAO Guoyan.Evaluation of cascading collapse for private mined zone groups[J].Journal of Natural Disasters,2007,16(5):91-95.
[10] 郭生茂,刘涛,程刚,等.基于RG法的空区群矿柱临界破坏条件研究[J].金属矿山,2014,43(8):125-128.
GUO Shengmao,LIU Tao,CHENG Gang,et al.Pillar critical failure condition of mined-out zone groups based on RG method[J].Metal Mine,2014,43(8):125-128.
[11] GHASEMI E,ATAEI M,SHAHRIAR K,et al.Assessment of roof fall risk during retreat mining in room and pillar coal mines[J].International Journal of Rock Mechanics and Mining Sciences,2012,54:80-89.
[12] GUARASCIO M,ORESTE P.Evaluation of the stability of underground rock pillars through a probabilistic approach[J].American Journal of Applied Sciences,2012,9(8):173.
[13] NAJAFI M,JALALI S M E,SERESHKI F,et al.Probabilistic analysis of stability of chain pillars in Tabas coal mine in Iran using Monte Carlo simulation[J].Journal of Mining and Environment,2016,7(1):25-35.
[14] WATTIMENA R K.Predicting the stability of hard rock pillars using multinomial logistic regression[J].International Journal of Rock Mechanics and Mining Sciences,2014(71):33-40.
[15] CAUVIN M,VERDEL T,SALMON R.Modelling uncertainties in pillar stability analysis[A].Symposium Post mining[C].2005.
[16] WATTIMENA R K,KRAMADIBRATA S,SIDI I D,et al.Developing coal pillar stability chart using logistic regression[J].International Journal of Rock Mechanics and Mining Sciences,2013,58:55-60.
[17] 刘彩平,王金安,侯志鹰.房柱式开采煤柱系统失效的模糊理论研究[J].矿业研究与开发,2008,28(1):8-9.
LIU Caiping,WANG Jin’an,HOU Zhiying.Study on failure of coal-pillar system in room-and-pillar mining based on fuzzy set theory[J].Mining Research and Development,2008,28(1):8-9.
[18] GHASEMI E,ATAEI M,SHAHRIAR K.Prediction of global stability in room and pillar coal mines[J].Natural Hazards,2014,72(2):405-422.
[19] POULSEN B A.Coal pillar load calculation by pressure arch theory and near field extraction ratio[J].International Journal of Rock Mechanics and Mining Sciences,2010,47(7):1158-1165.
[20] WANG F,ZHANG C,ZHANG X,et al.Overlying strata movement rules and safety mining technology for the shallow depth seam proximity beneath a room mining goaf[J].International Journal of Mining Science and Technology,2015,25(1):139-143.
[21] JIANG B,WANG L,LU Y,et al.Ground pressure and overlying strata structure for a repeated mining face of residual coal after room and pillar mining[J].International Journal of Mining Science & Technology,2016,26(4):645-652.
[22] 甘建东.膏体充填回收房柱式遗留煤柱方法研究[D].徐州:中国矿业大学,2014.
GAN Jiandong.Study on the recovery of the residual coal pillar in room and pillar goaf using the paste backfilling[D].Xuzhou:China University of Mining and Technology,2014.
[23] 李海清,向龙,贾宏宇.品字形房柱式采空区开采地表移动规律[J].地下空间与工程学报,2011,07(3):541-546.
LI Haiqing,XIANG Long,JIA Hongyu.The laws of surface movement in the pin-pillar style mining goaf area[J].Chinese Journal of Underground Space and Engineering,2011,3:023.
[24] 刘小平.房柱式采煤采空区稳定性评价方法与应用研究[D].北京:煤炭科学研究总院,2010.
LIU Xiaoping.Study and application of stability evaluation method for room and pillar coal goafs[D].Beijing:China Coal Research Institute,2010.
[25] KING H J,WHITTAKER B N.A review of current knowledge on roadway behaviour,especially the problems on which further information is required[A].Proceedings of the Symposium on Strata Control in Roadway (1970)[C].London:IME.1971:73-90.
[26] LARSON M K,LAVOIE T.Calibrating a caving model for sedi-mentary deposits—estimation of load distribution between gob and abutment[A].International Conference on Ground Control in Mining[C].2016.
[27] GALVIN J M.Interaction Between Workings[M].Springer International Publishing,2016:181-209.
[28] ZHANG P,HEASLEY K A.Elimination of boundary effect for laminated overburden model in pillar stability analysis[J].Journal of Central South University,2016,23(6):1468-1473.
[29] BISE C J.Modern American coal mining:Methods and applications[M].SME,2013.
[30] GALVIN J M,Hebblewhite BKSalamon MDG.UNSW Pillar stre-ngth determinations for Australian and South African Conditions[A].Proceedings of the 37th US rock Mechanics Symposium[C].1999:63-71.
[31] WAGNER H.Pillar design in coal mines[J].Journal of the South African Institute of Mining & Metallurgy,1980,80(1):37-45.
[32] MARK C.Pillar design methods for longwall mining[M].US Dept.of the Interior,Bureau of Mines,1990.
[33] SINGH R,MANDAL P K,SINGH A K,et al.Optimal underground extraction of coal at shallow cover beneath surface/subsurface objects:Indian practices[J].Rock Mechanics and Rock Engineering,2008,41(3):421-444.
[34] ZHU D,TU S.Mechanisms of support failure induced by repeated mining under gobs created by two-seam room mining and prevention measures[J].Engineering Failure Analysis,2017,82:161-178.