悬臂式掘进机是煤矿井下掘进工作面最重要的设备,主要用于巷道的挖掘,为布置采煤工作面做准备。随煤矿开采深度与机械化程度的不断提高[1-3],由于悬臂式掘进机安全,高效,灵活性高,适应性强等特点,其应用越来越广泛,尤其是纵轴式掘进机,在半煤岩巷道掘进中已得到普遍应用[4-6]。
在巷道掘进过程中,因断面内煤岩赋存条件和物理机械性质的复杂多变,导致所截割的煤岩硬度不断变化且具有较大的随机性。因此在截割臂水平或垂直摆动截割煤岩的过程中,截割头载荷也在连续复杂地变化[7-10]。理论上,当截割臂水平摆动截割时,其垂直摆角固定不变,截割头在断面内沿水平直线移动,但是复杂多变的截割头载荷会使截割臂的垂直摆角产生跳动现象;同样地,当截割臂垂直摆动截割时,其水平摆角也会在截割头载荷的作用下产生跳动现象。而这种截割臂摆角跳动现象对巷道断面边界规整度与巷道成形质量造成严重的影响[11-12]。因此,掌握固定截割方向截割臂摆角垂直跳动规律,对提高巷道成形质量及截割臂摆动作业自动控制有重要意义。
在对掘进机截割过程中截割臂动力学行为的研究方面,李晓豁等[7]基于Lagrange方程建立了掘进机整机动力学模型,通过构造虚拟截割头激励,进行了截割臂振动响应分析;张付凯等[13]基于Lagrange方程建立了截割臂水平摆动和垂直摆动的动力学模型,并通过迭代学习控制对截割臂运动轨迹进行控制;凌睿等[14-15]建立了掘进机截割臂横摆与径向伸缩数学模型,并采用滑模控制与二级滑模控制方法对截割臂的横摆角度和伸缩长度进行控制;DONG Z F等[16]通过有限元分析,研究了掘进机截割臂的振动特性及其影响因素;WANG J等[17]通过实体模型动力学仿真与实验,分析了掘进机截割臂振动特性及其动态负载;刘萍等[18]通过实体建模与仿真对截割臂进行了静力学特性研究,分析了截割头载荷作用下截割臂的应力-应变和变形情况。
截止到目前,对截割臂运动过程进行动力学建模的研究已有不少,但都是用于截割臂振动特性分析与摆动状态控制研究,而对截割臂摆角跳动的研究较少。针对该现状,以EBZ160型掘进机为例,基于Lagrange方程法,通过动力学建模与仿真求解分析,对固定截割方向截割臂摆角垂直跳动规律进行研究,并通过井下工程实验对仿真结果进行验证。
1 截割臂摆角跳动动力学模型
1.1 运动状态分析
理论上,由于煤矿井下工作环境极其复杂,悬臂式掘进机在截割过程中应该是一个有无限多个自由度的系统。因此,要建立掘进机截割臂摆角跳动动力学模型,必须对掘进机的工作状态进行合理、适当的简化与假设[19]。根据掘进机的实际结构和工作环境,对掘进机的工作状态作如下简化与假设:
(1)总体来说,掘进机各部分的质量分布比较均匀且弹性较小,故可忽略其弹性,将其简化为集中质量:截割头质量m1,截割臂质量m2,机体质量m3(包括行走机构);
(2)假设掘进机各部分之间通过无质量的弹性元件连接,其中截割头与截割臂之间的刚度用K1来表示,截割臂与机体之间的刚度用K2来表示;
(3)假设掘进机各部分之间的阻尼均为黏性阻尼,截割头与截割臂之间的阻尼用C1来表示,截割臂与机体之间的阻尼用C2来表示;
(4)本文研究的目标是固定截割方向下的掘进机截割臂摆角跳动规律,因此在确定截割头载荷时,没有必要对单个截齿的受力进行分析。可将截割头载荷简化为三向力,即水平方向,竖直方向以及垂直于煤壁方向的力。
以掘进机机体重心的初始位置为原点,建立三维直角定坐标系OXYZ,以掘进机机体重心为原点,建立固定于掘进机机体并随机体运动的动坐标系O′X′Y′Z′,如图1和2所示。X轴为水平方向,Y轴为垂直于煤壁方向,Z轴为竖直方向。
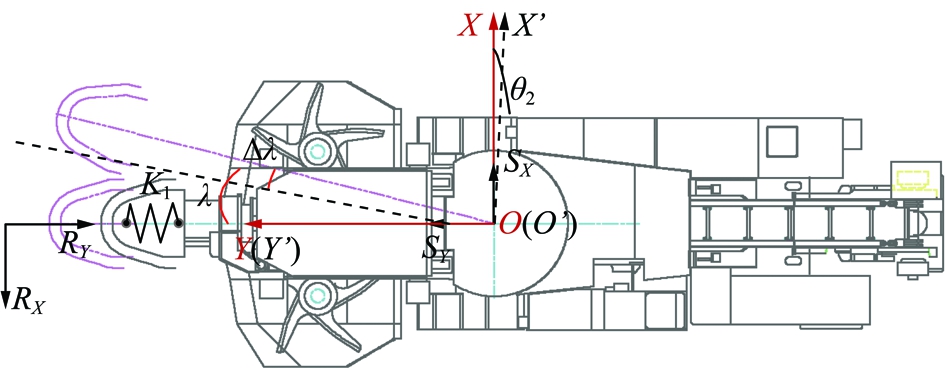
图1 截割臂水平摆动截割
Fig.1 Horizontally swing condition of the cutting arm
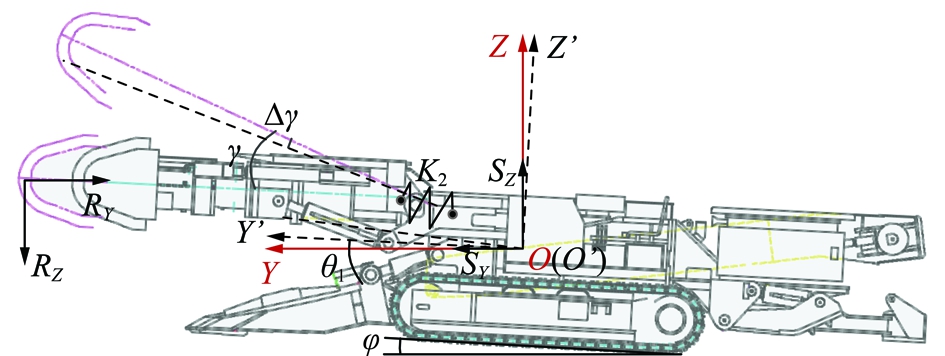
图2 截割臂垂直摆动截割
Fig.2 Vertically swing condition of the cutting arm
图1中,λ为截割臂相对于机体的水平摆角;Δλ为截割臂水平摆角跳动量;θ2为X轴与X′轴之间的夹角在定坐标系中XOZ平面内的投影;SX为O与O′之间的距离在定坐标系中X轴上的投影;SY为O与O′之间的距离在定坐标系中Y轴上的投影;RX为截割头载荷在水平方向的分力;RY为截割头载荷在垂直于煤壁方向的分力。图2中,γ为截割臂相对于机体的垂直摆角;Δγ为截割臂垂直摆角跳动量;θ1为Y轴与Y′轴之间的夹角在定坐标系中YOZ平面内的投影;SZ为O与O′之间的距离在定坐标系中Z轴上的投影;RZ为截割头载荷在竖直方向的分力;φ为煤层坡度角。
1.2 动力学模型
掘进机在截割过程中可以看作一个完整的系统,应用系统动力学Lagrange方程,可以建立截割臂摆角跳动的运动微分方程,从而精确描述掘进机截割过程中截割臂的动力学行为。
系统动力学第二类Lagrange方程[20]:
(1)
考虑黏性阻力,引入Rayleigh耗散函数D,则Lagrange方程变为
(2)
将有势力从式(2)右端分离出去,即引入势能函数U(qi),那么式(2)可以进一步变为
(3)
式中,T为系统的动能;D为系统的耗散能;U为系统的势能;i为广义坐标数;Qi为广义力。
以式(3)形式的Lagrange方程,在截割臂垂直摆动和水平摆动两种截割工况下,分别建立掘进机截割过程截割臂水平摆角跳动和垂直摆角跳动的动力学模型,并进行仿真求解分析。
截割臂垂直摆动截割工况下,其水平摆角跳动的运动微分方程推导过程如下:

(8)
将式(5)~(8)代入式(3),得到截割臂垂直摆动截割工况下,其水平摆角跳动动力学模型如下:
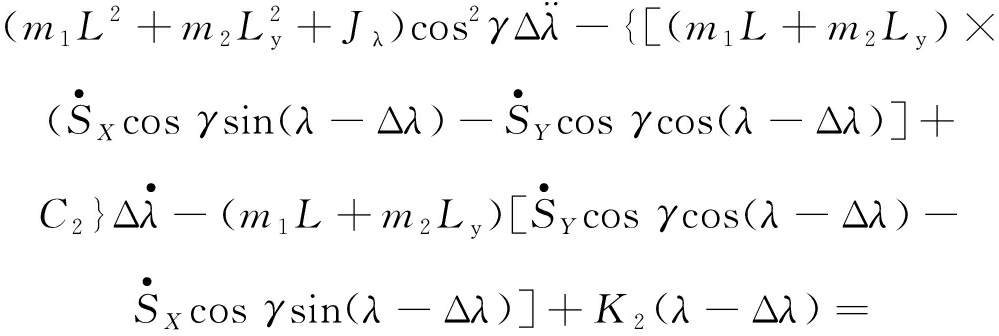
RXLcos γcos λ+MH
(9)
式中,L为截割臂回转中心与截割头回转中心的之间的距离;Ly为截割臂的重心与其回转中心之间的距离;Jλ为截割臂水平摆动时的转动惯量;MH为截割臂水平摆动驱动力矩。
截割臂水平摆动截割工况下,其垂直摆角跳动的运动微分方程推导过程如下:

K2(γ-Δγ)+K1{Lsin [(γ-Δγ)+φ-θ1]-
Lsin [(γ-Δγ)+φ]-bsin θ2+SYsin(φ-θ1)+
SZcos(φ-θ1)+SXsin θ2}×
{Lcos[(γ-Δγ)+φ-θ1]-Lcos[(γ-Δγ)+
φ]}/cos2(γ-Δγ)+K1sin(γ-Δγ)×
{Lsin [(γ-Δγ)+φ-θ1]-Lsin [(γ-Δγ)+
φ]-bsin θ2+SYsin(φ-θ1)+SZcos(φ-
θ1)+SXsin θ2}2/cos3(γ-Δγ)
(14)
将式(11)~(14)代入式(3),得到截割臂水平摆动截割工况下,其垂直摆角跳动动力学模型如下:
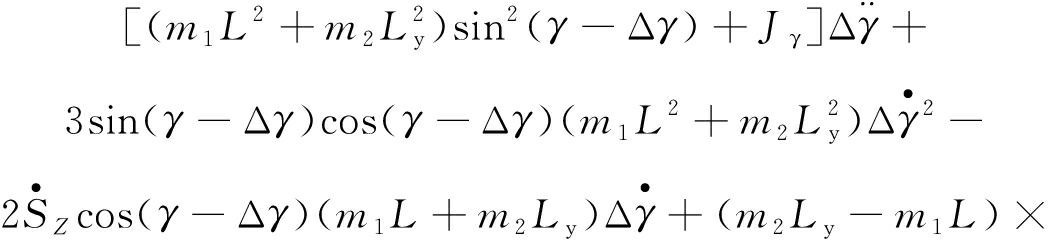
gcos[(γ-Δγ)+φ-θ1]+K2(γ-Δγ)+
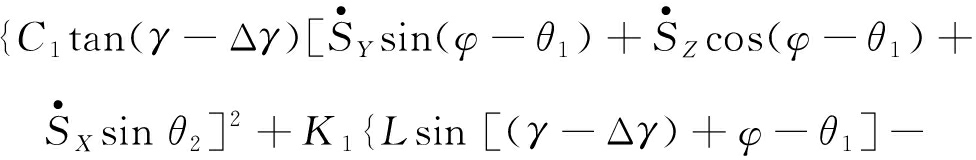
Lsin [(γ-Δγ)+φ]-bsin θ2+SYsin(φ-θ1)+
SZcos(φ-θ1)+SXsin θ2}{Lcos[(γ-Δγ)+
φ-θ1]-Lcos[(γ-Δγ)+φ]}+K1tan(γ-Δγ)×
{Lsin [(γ-Δγ)+φ-θ1]-Lsin[(γ-Δγ)+
φ]-bsin θ2+SYsin(φ-θ1)+
SZcos(φ-θ1)+SXsin θ2]2}}/cos2(γ-Δγ)=
RZLcos γcos λ+MV+MG
(15)
式中,b为掘进机机体长度的1/2;Jγ为截割臂垂直摆动时的转动惯量;MV为截割臂垂直摆动驱动力矩;MG为截割臂自身重力矩。
2 截割头载荷计算
由式(9)和(15)可知,要对掘进机截割臂摆角跳动动力学模型进行求解,必须先得到截割头载荷作为初始输入量。而掘进机截割过程中截割头载荷复杂多变的现状,决定了直接在现场获取截割头载荷谱的难度很大,个别研究人员获得的载荷谱也极其复杂且无规律,很难进行处理并被有效利用[21-22]。针对该现状,笔者提出了一种截割头载荷离散化计算方法。
掘进机截割臂水平摆动截割时由一对回转油缸驱动,垂直摆动截割时由一对升降油缸驱动,而随所截割煤岩硬度的不同,回转油缸与升降油缸的压力也在不断变化,且呈正相关关系[23]。回转油缸与升降油缸的压力可以用油缸压力传感器精确测量,因此,根据回转油缸和升降油缸的压力可以计算出截割头对煤壁的破碎力,根据牛顿第三定律,截割头对煤壁的破碎力即为该组油缸压力下的截割头载荷。
2.1 截割头载荷水平方向分力计算方法
掘进机截割臂固联于回转台上,由对称布置的水平回转油缸驱动。油缸杆与回转台相连,油缸筒与本体架相连。工作时,一侧油缸伸长另一侧油缸同步缩短,协同作用推动回转台转动,带动截割臂绕其回转中心水平摆动。如图3所示,回转台回转中心为O点;右侧油缸杆与回转台铰接点为A点,油缸筒与本体架铰接点为B点,左侧油缸筒与本体架铰接点为C点,油缸杆与回转台铰接点为D点;截割头受力点为R点;回转台回转半径为OA=OD=r,OB=OC=l1,OR=L1,∠AOB=∠COD=α。当截割臂水平摆动一定角度λ后,A点运动到A′点,D点运动到D′点,此时CD′=l2,A′B=l3。

图3 截割臂水平摆动二维图
Fig.3 Two-dimensional diagram of horizontal swing process
以截割臂水平向右摆动为例进行分析。水平向右摆动截割时截割头载荷在水平方向的分力水平向左,左侧油缸无杆腔进油对回转台外推,右侧油缸为有杆腔进油对回转台回拉,左侧外推力大于右侧回拉力。截割臂水平向左摆动截割时,受力情况与上述分析对称相反,此处不再赘述。
以回转台回转中心点O为基点,左侧油缸的外推力对点O的力矩为
MT=P1S1[rl1sin(α+λ)]/l2
(16)
右侧油缸的回拉力对点O的力矩为
ML=P1(S1-S2)[rl1sin(α-λ)]/l3
(17)
截割头载荷对点O的力矩为
M1=RXL1cos γcos λ
(18)
掘进机在钻进煤壁过程中,回转台承受较大的单侧压力,而在断面截割过程中,回转台承受压力很小且较为分散;并且回转台与回转支承之间为滚动轴承连接且润滑充足。因此,相对于驱动油缸的驱动力和煤壁作用于截割头的阻力,回转台自身摩擦力矩可忽略不计。联立式(16)~(18)得截割头载荷力在水平方向的分力为
式中,P1为回转油缸压力;S1为回转油缸缸径横截面积;S2为回转油缸杆径横截面积。
2.2 截割载荷竖直方向分力计算方法
截割臂垂直摆动截割时由一对平行对称布置的升降油缸驱动,油缸杆与截割臂相连,油缸筒与回转台相连。工作时,一对升降油缸同步伸长或缩短,推动截割臂上下摆动。如图4所示,截割臂与回转台铰接点为O′点;油缸筒与回转台铰接点为E点;油缸杆与悬臂铰接点为F点;截割头受力点为R点;O′E=l4,O′F=l5,O′R=L2,截割臂重心到O′的距离为LG,∠EO′F=β。当截割臂垂直摆动一定角度γ后,F点运动到F′点,此时EF′=l6。
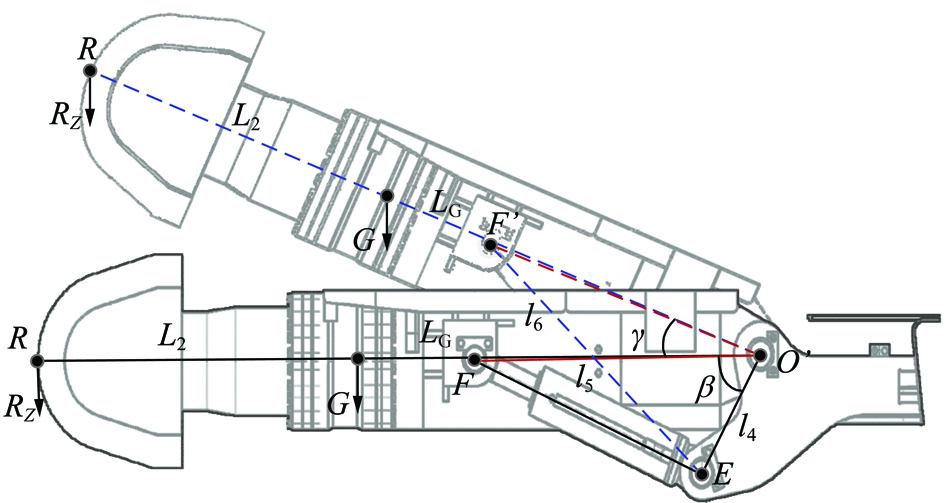
图4 截割臂垂直摆动二维图
Fig.4 Two-dimensional diagram of vertical swing process
以截割臂垂直向上摆动为例进行分析。垂直向上摆动截割时截割头载荷在竖直方向的分力竖直向下,升降油缸无杆腔进油将截割臂向上推。截割臂垂直向下摆动截割时,受力情况与上述分析对称相反,此处不再赘述。
以截割臂与回转台铰接点O′为基点,截割头载荷对点O′的力矩为
M2=RZL2cos λcos γ
(19)
截割臂自身重力对点O′的力矩为
MG=(m1+m2)gLGcos λcos γ
(20)
升降油缸驱动力对点O′的力矩为
(21)
联立式(18)~(20)得截割头载荷在竖直方向的分力为
式中,P2为升降油缸压力;S3为升降油缸缸径横截面积。
2.3 截割头载荷计算结果
基于井下工程性实验,在EBZ160型掘进机上测取截割臂回转驱动油缸和升降驱动油缸油路中的压力,并对实测数据进行处理。在截割过程中,回转驱动油缸压力在5~21 MPa变化,如图5所示;根据回转驱动油缸压力和截割臂水平摆角对截割头载荷在水平方向的分力RX进行仿真计算,结果如图6所示。升降驱动油缸压力在8~21 MPa变化,如图7所示;根据升降驱动油缸压力和截割臂垂直摆角对截割头载荷在竖直方向的分力RZ进行仿真计算,结果如图8所示。
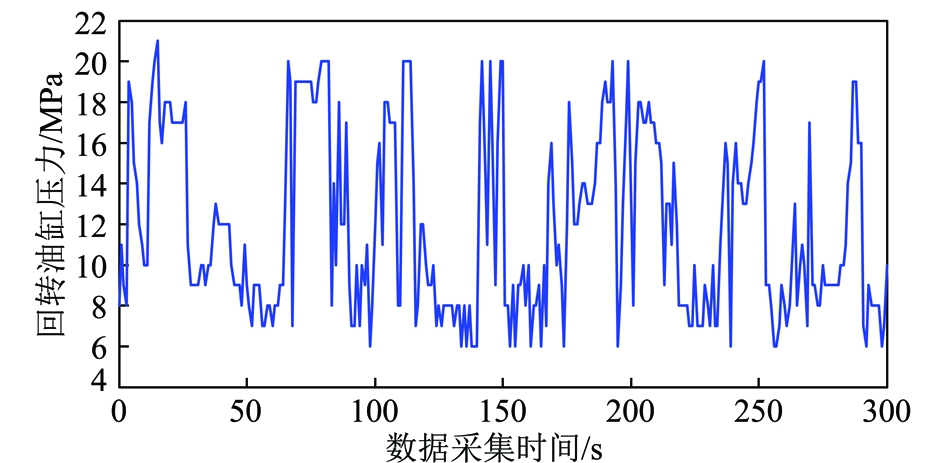
图5 回转油缸压力
Fig.5 Pressure of angling cylinder
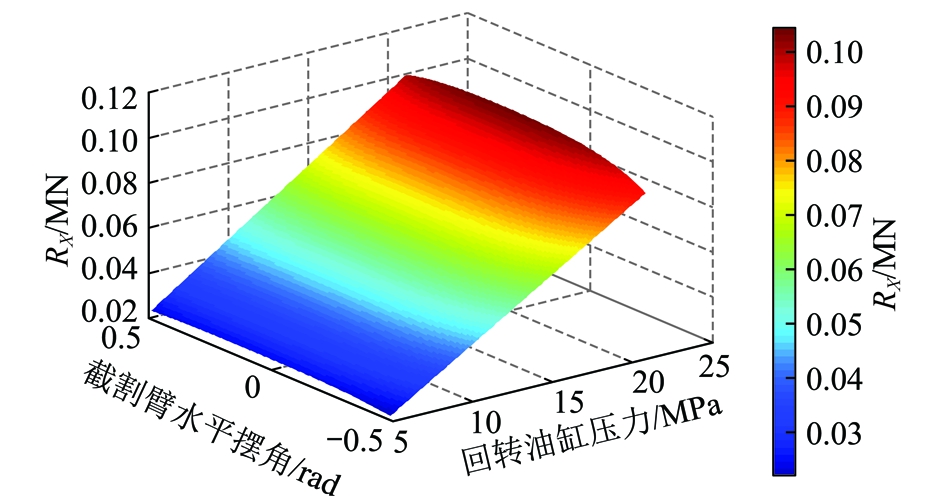
图6 截割头载荷水平分力RX
Fig.6 Horizontal force RX of the cutting head load

图7 升降油缸压力
Fig.7 Pressure of lifting cylinder
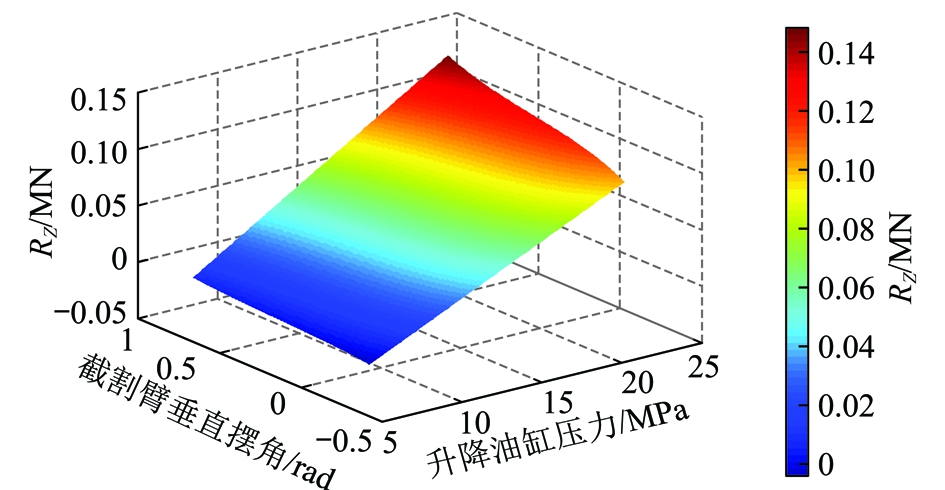
图8 截割头载荷竖直分力RZ
Fig.8 Vertical force RZ of the cutting head load
3 仿真分析与实验验证
3.1 Simulink模型及仿真条件设定
根据截割臂水平摆角跳动动力学模型和垂直摆角跳动动力学模型,即式(9)和(15),在Matlab/Simulink中分别建立求解微分方程的仿真模型,如图9和10所示。

图9 截割臂水平摆角跳动求解仿真模型
Fig.9 Simulation model of solving cutting arm’s horizontal swing angle run-out
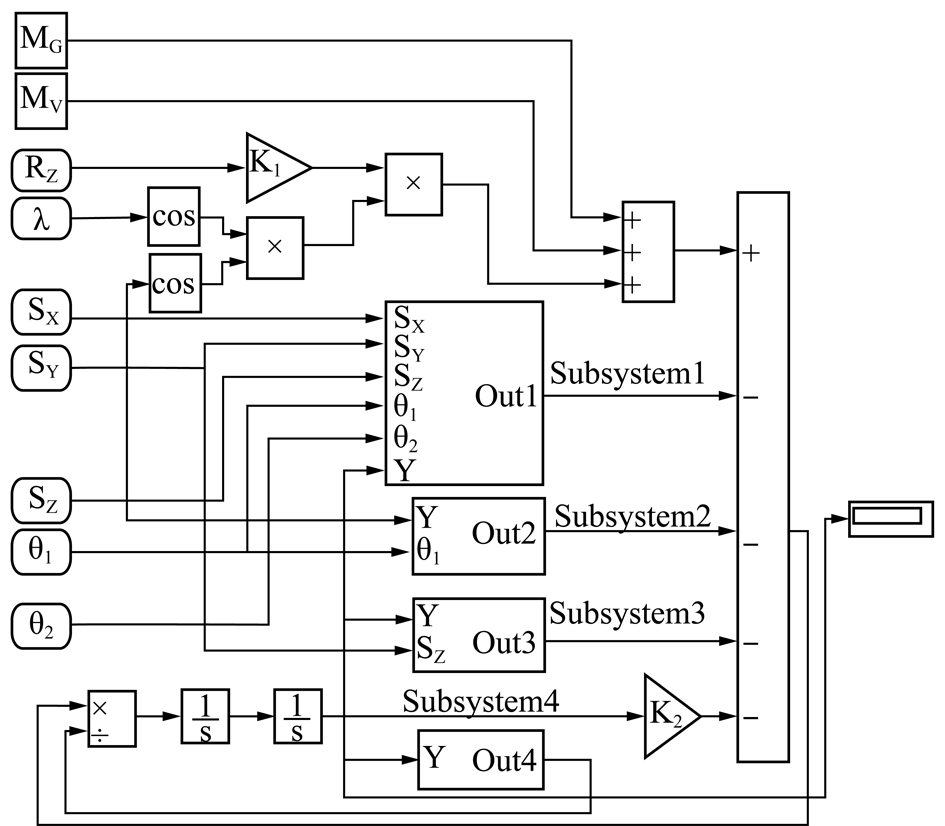
图10 截割臂垂直摆角跳动量求解仿真模型
Fig.10 Simulation model of solving cutting arm’s vertical swing angle run-out
EBZ160型掘进机截割臂水平左右摆动的最大摆角均为28°;垂直向上摆动的最大摆角为38°,向下摆动的最大摆角为24°。因此,求解截割臂水平摆角跳动动力学模型时,选取γ=-24°,-12°,0°,20°和38°五种截割位置;求解截割臂垂直摆角跳动动力学模型时,选择λ=-28°,-14°,0°,14°和28°五种截割位置。仿真初始参数见表1[24-26]。
表1 仿真初始参数
Table 1 Parameters of simulation’s input

3.2 井下工程实验
井下实测机型为EBZ160型悬臂式掘进机,实验地点为冀中能源邢东矿,该矿井深度在580~1 200 m,综掘工作面条件较好,适合安装各类传感器对掘进机进行工作状态监测。
选用本安型GUC360矿用倾角传感器测取截割臂的垂直摆角;选用抗噪声干扰能力强、测试稳定性好的W18LD型双路测速传感器测取截割臂的水平摆角;选用满足井下煤安规程要求的BYD-60型矿用隔爆型压力变送器测取升降驱动油缸和回转驱动油缸油路中的压力。所有检测到的数据均存储在机载大容量数据记录仪中。实验设备实物如图11所示。

图11 实验设备实物
Fig.11 Pictures of the experimental equipment
测量截割臂水平摆角时,根据掘进机回转台实际结构,在回转台内侧环面一定弧长范围内安装2套钢铁齿条,一套齿条固定不动,另一套齿条随回转台转动,齿条齿宽为4 mm,对应截割臂水平摆动角度为1°。将W18LD型双路测速传感器敏感面对准齿条,作用距离为0~2 mm,如图12所示。随回转台的转动,双路测速传感器可直接输出截割臂水平摆角信号。
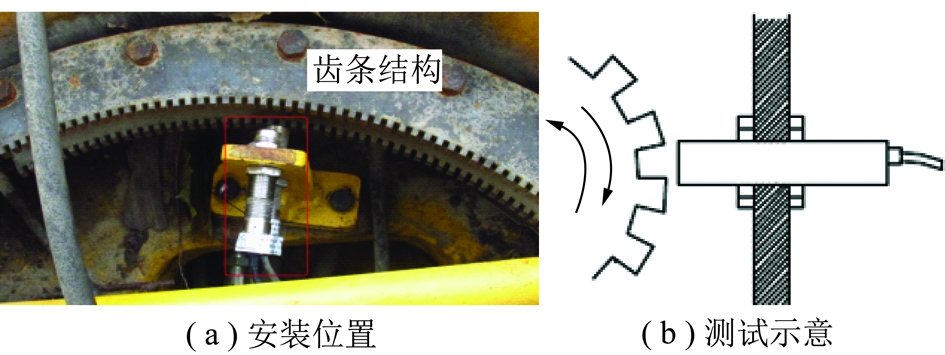
图12 双路测速传感器安装位置与测试示意
Fig.12 Installation position of dual speed sensor and the test schematic diagram
3.3 仿真与实验结果分析
将掘进机截割臂水平摆角跳动动力学模型仿真求解结果与对应的截割头载荷进行曲线拟合处理,并与实验结果进行对比,如图13所示;再将其与截割头载荷RX及截割臂垂直摆角γ进行曲面拟合处理,结果如图14所示。
截割臂垂直摆动截割时,理论上要求其水平摆角λ固定不变,但由于不断变化的截割头载荷水平方向分力RX的作用,截割臂水平摆角λ会发生小幅度的变化,即产生一个跳动量Δλ,而该跳动量Δλ受截割头载荷RX与截割臂垂直摆角位置γ的共同影响。由图13可知,截割臂垂直摆动截割工况下,其水平摆角跳动仿真结果与实验结果基本一致。在任意垂直摆角γ的截割臂位置,随截割头载荷RX的增大,其水平摆角跳动量Δλ均是先减小后增大;Δλ的最大值可达到5.3°左右,最小值为0.5°左右;在不同垂直摆角γ的截割臂位置,使Δλ达到最小值的截割头载荷RX值不同,其范围为65~85 kN。由图14可知,随截割臂垂直摆角γ的增大,Δλ先增大后减小,约在γ=20°时达到最大值。

图13 截割臂水平摆角跳动与截割头载荷关系曲线
Fig.13 Curves of relationship between the cutting arm’s horizontal swing angle run-out and the cutting head load

图14 截割臂水平摆角跳动变化曲面
Fig.14 Changing surface of the cutting arm’s horizontal swing angle run-out
将掘进机截割臂垂直摆角跳动动力学模型仿真求解结果与对应的截割头载荷进行曲线拟合处理,并与实验结果进行对比,如图15所示;再将其与截割头载荷RZ及截割臂水平摆角λ进行曲面拟合处理,结果如图16所示。

图15 截割臂垂直摆角跳动与截割头载荷关系曲线
Fig.15 Curves of relationship between the cutting arm’s vertical swing angle run-out and the cutting head load
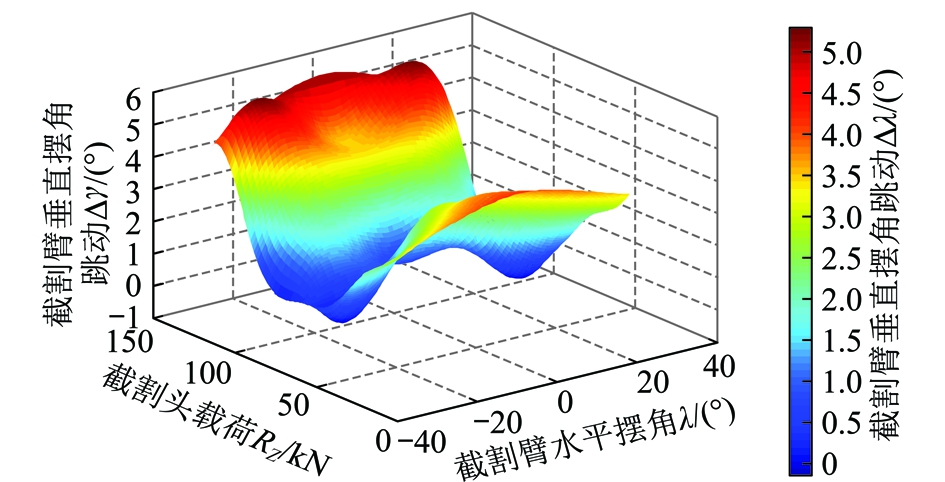
图16 截割臂垂直摆角跳动变化曲面
Fig.16 Changing surface of the cutting arm’s vertical swing angle run-out
同理,截割臂水平摆动截割时,理论上要求其垂直摆角γ固定不变,但因不断变化的截割头载荷竖直方向分力RZ的作用,截割臂垂直摆角γ会发生小幅度的变化,即产生一个跳动量Δγ,而该跳动量Δγ受截割头载荷RZ与截割臂水平摆角位置λ的共同影响。由图15可知,截割臂水平摆动截割工况下,其垂直摆角跳动仿真结果与实验结果基本一致。在任意水平摆角λ的截割臂位置,随截割头载荷RZ的增大,其垂直摆角跳动量Δγ均是先减小后增大;Δγ的最大值可达到5.4°左右,最小值为0.3°左右;在不同水平摆角λ的截割臂位置,使Δγ达到最小值的截割头载荷RZ值不同,其范围为55~100 kN。由图16可知,随截割臂水平摆角λ的增大,Δγ基本呈线性减小。
4 结 论
(1)提出了一种截割头载荷计算方法,根据力矩平衡原理,得到了截割头载荷与回转驱动油缸、升降驱动油缸压力及截割臂摆角之间的关系。根据井下实测的回转驱动油缸与升降驱动油缸压力数据进行仿真计算,得到了不同油缸压力下与不同截割臂摆角位置的截割头载荷谱。
(2)基于Lagrange方程法,针对掘进机截割臂水平摆动与垂直摆动截割两种工况,推导出截割臂摆角跳动二阶微分方程,建立了截割臂摆角跳动动力学模型与相应的Simulink仿真模型。将截割头载荷与截割臂摆角作为自变量,对截割臂摆角跳动动力学模型进行仿真求解,并对仿真求解结果进行处理与分析,得到了固定截割方向掘进机截割臂摆角垂直跳动规律。基于井下工程实验,完成井下综掘工作面掘进机工作状态数据采集,对实验数据进行处理并与仿真结果进行对比,验证了截割臂摆角跳动动力学模型及截割臂摆角跳动规律的正确性。
(3)截割头载荷是根据回转和升降驱动油缸压力及截割臂摆角计算所得,而这些参数的数据可以实时检测获取,因此固定截割方向掘进机截割臂摆角垂直跳动规律的研究,可以为进一步研究截割臂自动控制与截割头空间位置纠偏等问题提供借鉴。
参考文献(References):
[1] WANG Jinhua.Development and prospect on fully mechanized mining in Chinese coal mines[J].International Journal of Coal Science & Technology,2014,1(3):153-260.
[2] HARGRAVE Chad O,JAMES Craig A,RALSTON Jonathon C.Infrastructure-based localisation of automated coal mining equipment[J].International Journal of Coal Science & Technology,2017,4(3):252-261.
[3] WANG Jinhua,YU Bin,KANG Hongpu,et al.Key technologies and equipment for a fully mechanized top-coal caving operation with a large mining height at ultra-thick coal seams[J].International Journal of Coal Science & Technology,2015,2(2):97-161.
[4] 田劼,王苏彧,吴淼,等.悬臂式掘进机空间位姿的运动学模型与仿真[J].煤炭学报,2015,40(11):2617-2622.
TIAN Jie,WANG Suyu,WU Miao,et al.Spatial pose kinematics model and simulation of boom-type roadheader[J].Journal of China Coal Society,2015,40(11):2617-2622.
[5] YANG Yang,LI Guowei,YUAN Aihui.Performance analysis of a hybrid power cutting system for roadheader[J].Mathematical Problems in Engineering,2017,16(1):1-12.
[6] 魏晓华,师建国.纵轴式掘进机截割过程动力学建模与仿真[J].辽宁工程技术大学学报(自然科学版),2013,36(1):89-92.
WEI Xiaohua,SHI Jianguo.Dynamic modeling and simulation of cutting process for longitudinal roadheaders[J].Journal of Liaoning Technical University(Natural Science),2013,36(1):89-92.
[7] 李晓豁,何洋,李婷,等.纵轴式掘进机横向和纵向随机振动响应的分析[J].煤炭学报,2014,39(3):580-585.
LI Xiaohuo,HE Yang,LI Ting,et al.Analysis of horizontal and vertical random vibration responses of longitudinal roadheader[J].Journal of China Coal Society,2014,39(3):580-585.
[8] 杨健健,符世琛,吴淼,等.基于模糊判据的煤岩性状截割硬度识别[J].煤炭学报,2015,40(S2):540-545.
YANG Jianjian,FU Shichen,WU Miao,et al.Recognition of cutting hardness of coal rock properties based on fuzzy criteria[J].Journal of China Coal Society,2015,40(S2):540-545.
[9] 孙华飞,杨永明,鞠杨,等.开挖卸荷条件下煤岩变形破坏与能量释放的数值分析[J].煤炭学报,2014,39(2):258-272.
SUN Huafei,YANG Yongming,JU Yang,et al.Numerical analysis of deformation,failure and energy release mechanisms of fractured coal rock under unloading conditions[J].Coal Mine Machinery,2014,39(2):258-272.
[10] 李晓豁.横轴式掘进机横向截割的动力学行为研究[J].中国工程机械学报,2005,3(1):73-75.
LI Xiaohuo.Study of dynamic behaviour of horizontal-axial-roadheader as transverse cutting[J].Chinese Journal of Construction Machinery,2005,3(1):73-75.
[11] 田劼,杨阳,吴淼,等.纵轴式掘进机巷道断面自动截割成形控制方法[J].煤炭学报,2009,34(1):111-115.
TIAN Jie,YANG Yang,WU Miao,et al.Automatic section cutting and forming control of longtitudinal-axial-roadheaders[J].Journal of China Coal Society,2009,34(1):111-115.
[12] 王苏彧,高峰,吴淼,等.基于PCC的任意巷道断面自动截割成形控制系统[J].煤炭学报,2013,38(S1):261-266.
WANG Suyu,GAO Feng,WU Miao,et al.Control system of automatic arbitrary roadway section cutting and forming based on PCC[J].Journal of China Coal Society,2013,38(S1):261-266.
[13] 张付凯,王福忠,高庆华.掘进机截割臂运动轨迹的迭代学习控制[J].电子测量与仪器学报,2014(12):1355-1362.
ZHANG Fukai,WANG Fuzhong,GAO Qinghua.Cutting arm trajectory control of roadheader based on adaptive iterative learning[J].Journal of Electronic Measurement and Instrumentation,2014(12):1355-1362.
[14] 凌睿,柴毅,李大杰,等.掘进机器人截割臂建模与控制[J].系统仿真学报,2009,21(23):7601-7604,7608.
LING Rui,CHAI Yi,LI Dajie,et al.Modeling and control for arm of roadheader robot[J].Journal of System Simulation,2009,21(23):7601-7604,7608.
[15] 凌睿,柴毅.悬臂式掘进机器人截割臂建模与二阶滑模控制器设计[J].控制理论与应用,2010,27(8):1037-1046.
LING Rui,CHAI Yi.Dynamic modeling and design of second-order sliding-mode controller for arm of roadheader robot[J].Control Theory & Applications,2010,27(8):1037-1046.
[16] DONG Z F,WANG T H,LIU J,et al.The modal analysis with finite element method for the cutting arm of EBZ160 roadheader[J].Applied Mechanics and Materials,2013,397-400:405-408.
[17] WANG J,ZHANG Y,DONG L.Analysis of vibration characteristics and dynamic load identification in continuous miner cutting arm[J].International Journal of Simulation-Systems,Science & Technology,DOI 10.5013/IJSSST.a.17.13.20.
[18] 刘萍.掘进机截割臂静力学特性研究[J].煤矿机械,2014(2):61-63.
LIU Ping.Research on static characteristics of cutting arm of roadheader[J].Coal Mine Machinery,2014(2):61-63.
[19] 李晓豁.掘进机截割的关键技术研究[M].北京:机械工业出版社,2008.
[20] 杨义勇,金德闻.机械系统动力学[M].北京:清华大学出版社,2009.
[21] 刘春生,王庆华,任春平.镐型截齿载荷谱定量特征的旋转截割实验与仿真[J].黑龙江科技大学学报,2014,24(2):195-199.
LIU Chunsheng,WANG Qinghua,REN Chunping.Research on quantitative characteristics of conical pick load spectrum based on rotary cutting experiments and simulation[J].Journal of Heilongjiang University of Science & Technology,2014,24(2):195-199.
[22] 刘春生,赵英好,王庆华.截煤工况下镐型截齿的自旋转力学机理[J].黑龙江科技大学学报,2014,24(1):75-80,90.
LIU Chunsheng,ZHAO Yinghao,WANG Qinghua.Self-rotation mechanical mechanism of conical bit from cutting coal condition[J].Journal of Heilongjiang University of Science & Technology,2014,24(1):75-80,90.
[23] 宋月辉.EBZ160B薄煤层掘进机整机动力仿真和关键结构件有限元分析[D].石家庄:河北科技大学,2014.
SONG Yuehui.Dynamic simulation and finite element analysis of key structural parts for EBZ 160B roadheader[D].Shijiazhuang:Hebei University of Science and Technology,2014.
[24] 哈尔滨工业大学理论力学研究室.理论力学I[M].北京:高等教育出版社,2009.
[25] 陈媛媛.履带车辆行动系统动力学仿真分析[D].沈阳:沈阳理工大学,2012.
CHEN Yuanyuan.The dynamic analysis and simulation of tracked vehicles[D].Shenyang:Shenyang Ligong University,2012.
[26] 王佩勋.悬臂式掘进机横向截割时稳定性研究[J].煤矿机械,2009(5):64-66.
WANG Peixun.Study on stability for transverse-cutting of cantilevered roadheader[J].Coal Mine Machinery,2009(5):64-66.