移动阅读
移动阅读
岩石在拉力状态或者较低压力水平下会出现Ⅰ 型拉破坏，随着压力逐渐上升岩石破坏模式从拉破坏向剪切破坏过渡。随着围压的逐渐加大，剪切带周边翼状裂纹逐渐减少，破坏中拉破坏的影响逐渐降低，破坏模式向剪切破坏过渡，滑移面角度向理论破坏角度靠拢，剪切面粗糙度降低[1]。当压力继续增大时，部分孔隙岩石出现了与最大主应力方向正交的压密屈服带，且屈服强度随着平均应力的增长而降低。深部扰动诱发岩石破坏模式在高应力水平下从常规剪切破坏向孔隙坍塌型破坏转化。
高应力下，岩体材料的非线性行为更加突出，岩体原位应力状态与地应力环境作用更加突显，不同工程活动方式诱发的高应力和高量级的灾害更加凸显。基于浅部的经验和研究建立起来的理论体系与深部岩体力学特性有较大的差异。迫切需要与深部实际环境和不同工程活动方式相关联的深部岩石力学理论，破解深部资源开采的理论与技术难题。
在岩石、岩体力学强度理论方面，应用较广的理论主要有Mohr-Coulomb(MC)强度理论、Hoek-Brown(HB)强度准则及基于以上强度理论演化的强度模型[2-5]。
MC 准则的一个严重限制是当一个主应力是拉伸时需要一个拉伸截断。HB准则是在主应力空间中描述了不受中间主应力影响的各向同性岩石随着围压的增加峰值强度增加的非线性破坏准则。但是深部开采条件下的岩石、岩体强度理论研究需要探索破坏模式过渡的内在机理，需要分析中间主应力对强度的影响特征和静水压力下深部岩石屈服条件[6]。考虑中间主应力，Paul-Mohr-Coulomb(PMC)准则被提出并发展，其模型能表征岩土材料随应力条件上升由拉断破坏向剪切破坏转变的机制。本文基于PMC准则，考虑多孔岩石裂隙坍塌的特征和岩石破坏模式的转化，提出了高应力下表征压剪屈服的Back-Paul-Mohr-Coulomb(BPMC)模型。
考虑中间主应力影响，由Paul(1968)提出，并由Meyer和Labuz(2013)[7]实现的PMC准则，表达式如下:
NcσΙ-(Nc-Ne)σⅡ-(Ne+1)σⅢ=V0
(1)
式中，Nc=(1-sin φc)/(2sin φc),φc为三轴伸长(σ1=σ2)时的内摩擦角;Ne=(1-sin φe)/(2sin φe)，φe为三轴伸长(σ2=σ3)时的内摩擦角;V0为理论各向同性抗拉强度。即其表达方式如下:
(2)
其主应力空间中的六面锥体破坏面如图1所示。
针对岩石材料的破坏机理转化特征，ISSEN和RUDNICKI(2000)建议采用双屈服组合模型进行分析;而为了捕捉岩土材料破坏模型的凸起特点，LABUZ团队以PMC模型为基础发展出十二面椎体PMC模型[7-8]。PMC破坏准则以分段线性的方式，通过对2个平面(图2)拟合构成十二边形破坏面，可近似地看成一个非线性的破坏表面。该模型需要6个材料参数，分别是表征P1平面(剪破坏)的材料参数
和P2平面(拉破坏)的材料参数
十二边形PMC破坏准则可以写为
(3)
(4)
该模型能够表征岩石材料随应力条件上升由拉断破坏向剪切破坏转变的机制。在p-q平面和π平面中，随着平均应力的变化，破坏表面形状发生过渡。低围压情况下，岩体破坏表现为拉破坏;较高围压情况下，岩体表现为剪破坏。
图1 六面锥体PMC模型
Fig.1 Six-sided pyramidal PMC model
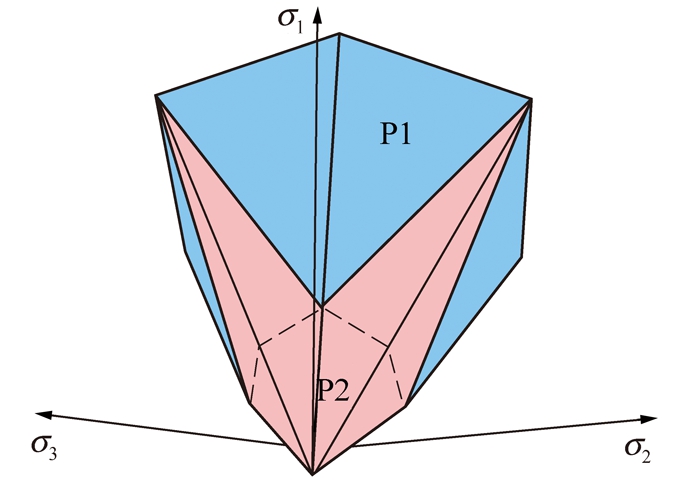
图2 十二边形PMC模型
Fig.2 Twelve-sided pyramidal PMC model
图2(图片来自LABUZ(2018)[9])表示了从6边形到12边形锥体破坏面再转换至6边形的锥体破坏表，其中
在较低的平均应力条件下，P2面控制着破坏，随着平均应力的增加，P2面与P1面在压缩端相交，六边形破坏面转换为十二边形破坏面。当平均应力继续增加，P1面控制着破坏。
多孔岩石从剪切破坏到压密屈服的过渡问题颇受关注[10-11]。多孔岩石在低、高平均应力和不同荷载条件下的力学响应试验研究对于岩体内部结构的设计至关重要。脆性区域内岩石的破坏本质上是与应变局部化相关的剪切破裂现象。对于高平均应力下的多孔岩石，研究观察到的失效模式通常伴有压实带、颗粒破裂和孔隙坍塌[12-13]。
将Mohr-Coulomb强度理论应用于微观分析中，多孔岩石的结构可以看作是堆砌单元的砖石结构(图3(a))。在岩体的圆形隧道中，不同的边界应力会产生不同的局部应力分布，不同的局部应力集中会导致单元的不同破坏模式(图3(b)，分别代表拉伸破坏、剪切破坏和塑性破坏)。
图3 多孔岩石破坏示意
Fig.3 Destruction of porous rock
在低围压下，岩石试样的破坏模式通常是由拉伸裂缝的发展控制的。当围压增加，剪切破坏成为岩石材料常见的破坏形式。围压继续均匀增加，单元内部静水压力可能导致孔隙周围出现一定的塑性破坏区域。不同的单元破坏模式会导致不同的宏观破坏类型(图4)。
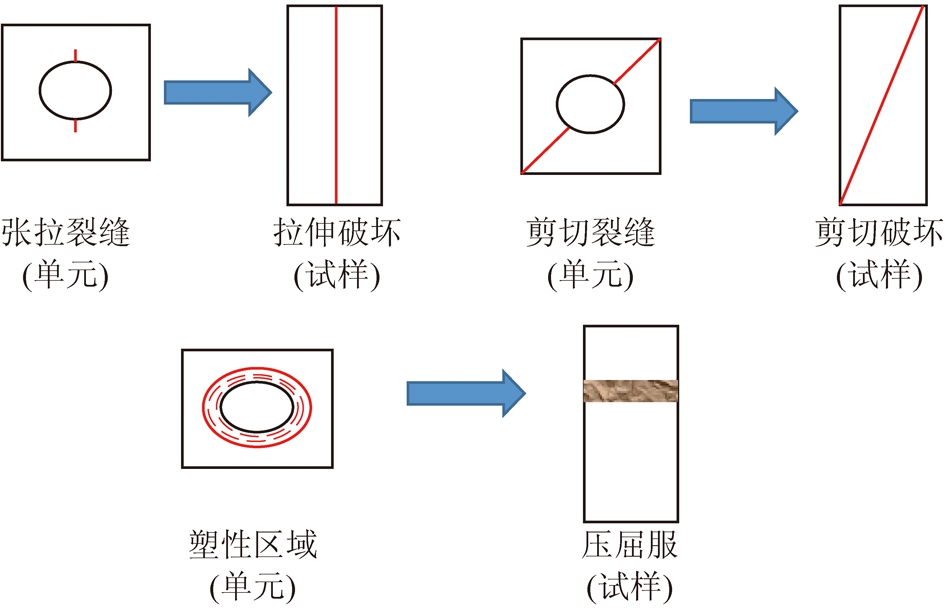
图4 微观破坏模式导致宏观破坏类型
Fig.4 Micro-destruction mode leads to macro damage type
对于多孔隙岩石，如果岩石中的孔洞空间足够大，则塑性区会不断发育，最终发生压屈服。一定的静水压力会引起多孔岩石的孔隙坍塌。一个“帽子”屈服面出现并影响应力空间中的抗剪强度包络线。
ALI，李远等通过对白垩岩进行不同围压条件下的三轴试验，得到了白垩岩试件随着压力上升出现的破坏模式过渡特征，其实验结果如图5,6所示[14]。图5中，随着围压的增加，试样破坏面、破坏角和破坏类型发生变化；4号试样为围压5 MPa的破坏情况，出现过渡型破坏面，破坏角为36°；5号试样为围压10 MPa的破坏情况，试样出现明显压密带。图6中，路径(i)到路径(iv)分别为无预压力、10 MPa预压力、30 MPa预压力和60 MPa预压力情况下的白垩岩在10 MPa围压下的强度曲线，虚线表示屈服表面；从路径(i)到路径(iv)，帽子破坏面扩展并向右移动，硬化的试样其破坏模式发生变化。白垩岩塑性硬化后其强度包络线上的“帽子”屈服面与硬化后的黏聚力、摩擦角发展规律完全不同于土力学，而岩石力学中尚缺少相关研究。基于白垩岩孔隙坍塌规律，将摩擦强度理论应用于孔隙坍塌分析，提出BPMC模型。
图5 白垩岩不同压力下的破坏模式过渡
Fig.5 Failure mode transition of Mons chalk under different pressures
图6 10 MPa围压下不同预压力硬化下的白垩岩强度曲线
Fig.6 Failure curve of Mons chalk with increase in precom-paction stress for specimens failed under σ3=10 MPa
基于PMC模型理论，考虑岩石破坏模式的转化，提出了高应力下表征压剪屈服BPMC模型的公式形式。BPMC模型用3个主应力可以表示为
A1σΙ+B1σⅡ+C1σⅢ=1
(5)
其中,A1,B1,C1为材料参数。其中材料参数可以通过单轴压缩，等压屈服强度和单轴抗拉强度得到
(6)
其中,
为单轴压缩强度;
为等压屈服强度;
为单轴抗拉强度。
通过试验结果画出莫尔圆可得到2个内摩擦角和一个共同的顶点(图7(a))。图7(b)是在p-q平面中轴对称压缩和伸长条件下的PMC和BPMC的破坏包络线的示意图。在p-q平面中BPMC的线性破坏准则可以写为
(7)
式中，
为截距，常规压缩实验下为
常规压缩实验下为
三轴实验下为
(8)
破坏包络线有3个材料参数，即压缩时的内摩擦角
伸长时的内摩擦角
和等压屈服点
材料参数可以通过高应力条件下的三轴压缩和三轴伸长试验得到。三轴压缩条件为σⅠ=σa和σⅡ=σⅢ=σr，环向施加稳定围压，增加轴压直至岩石破坏；三轴伸长条件为σⅠ=σⅡ=σr和σⅢ=σa，环向施加稳定围压，逐渐降低轴压直至岩石破坏(σa为轴压，σr为围压)。
图7 PMC和BPMC模型的破坏包络线的示意
Fig.7 Destruction envelope of PMC and BPMC models
考虑到多孔岩石不是理想的弹塑性或者弹脆性材料，理想的压屈服线为曲线，BPMC模型采用分段线性方式拟合压屈服线。图8代表p-q平面中12边形PMC&BPMC模型的破坏包络线的示意图。在p-q平面中，12边形BPMC的线性破坏准则可以写为
(9)
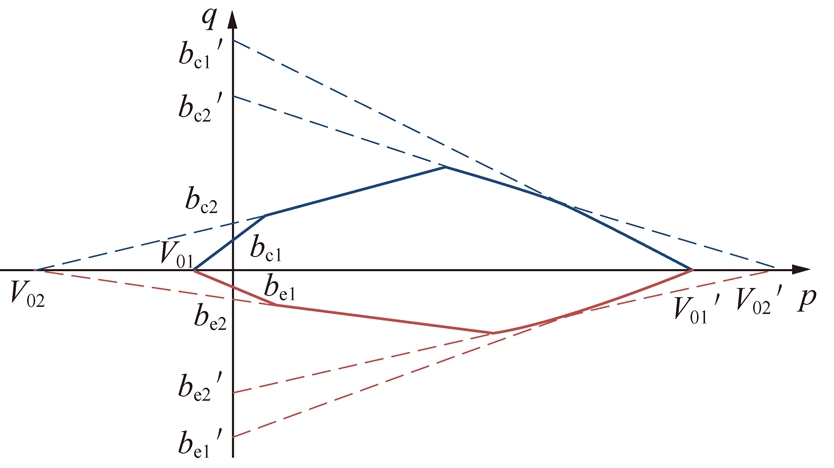
图8 PMC&BPMC模型的破坏包络线
Fig.8 Failure envelope of PMC and BPMC
曾飞涛，李远等[15]基于在p-q平面的应力不变量关系的转换提出了一种新的拟合方法。本文基于该方法进行BPMC参数获取方式的推导。
将破坏包络线
转化为直角坐标系，用
和θ表示
(10)
多轴压缩中
轴对称压缩中
轴对称伸长中
因此方程可以写为
(11)
可得到为
(12)
式中,
则p-q平面中BPMC破坏准则的一般方程式可以写为
(13)
通过试验得到轴对称和多轴条件下强度数据表示为(σΙ,σⅡ,σⅢ)，计算每种应力状态下的pn,qn和θn并代入方程(13)。可以生成一组形式为Ax=B的线性方程组:
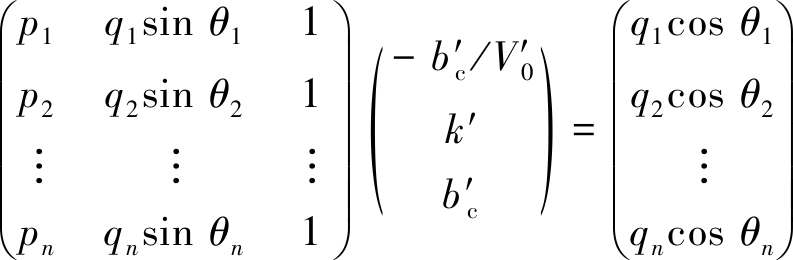
(14)
利用最小二乘法求解方程可以得到
求得
和求得
和k′。根据式(15)可解得压缩时的内摩擦角
伸长时的内摩擦角
(15)
根据两组压缩摩擦角
伸长内摩擦角和等压屈服点
绘制十二边形的BPMC模型。
为了验证PMC&BPMC准则及对应破坏模式转化理论的合理性，本文基于LABUZ团队数据[14]进行PMC&BPMC模型的拟合，对比拟合破坏面与试验数据；其次选用四川黄砂岩和金川大理岩，进行室内三轴压缩试验，研究不同围压下岩石破坏特征和强度特征。
根据上述方法，对试验数据进行处理，获取岩石参数见表1。
表1 岩石PMC&BPMC参数
Table 1 Rock PMC&BPMC parameters
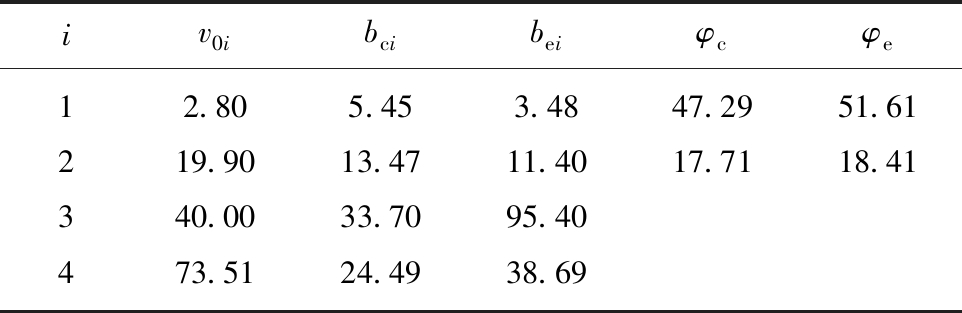
iv0ibcibeiφcφe12.805.453.4847.2951.61219.9013.4711.4017.7118.41340.0033.7095.40473.5124.4938.69
注:数据基于LABUZ团队[14]。
对PMC&BPMC的三维破坏面进行拟合，获得破坏表面和破坏包络线如图9～11所示。
图9 空间拟合屈服面和p-q平面的截面
Fig.9 Space fitting yield surface and p-q plane
图10 PMC&BPMC模型在p-q空间形状及数据拟合
Fig.10 PMC&BPMC model in p-q space and data fitting
该模型可用于预测和分析孔隙岩石帽子屈服面和破坏模式过渡的研究。在低围压情况下，岩石以拉破坏和剪切破坏为主。随着围压的逐渐加大，破坏模式向剪切破坏过渡;当压力继续增大时，岩石由剪切破坏向压密屈服破坏过渡。
图11 不同平均压力PMC&BPMC模型的π平面强度线
Fig.11 π plane strength line of PMC&BPMC model under different average pressures
3.2.1 试验方案
根据《水利水电工程岩石试验规程》(SL264-2016)中的相关规程，选取质地均匀、结构完整性好的四川黄砂岩、金川大理岩加工成φ30 mm×60 mm 的标准岩石试样(图12)，试样精度满足ISRM国际岩石力学学会要求。
图12 四川黄砂岩试样和金川大理岩试样
Fig.12 Sichuan yellow sandstone specimen and Jinchuan marble specimen
试验采用北京科技大学土木与资源工程学院地应力测量教育部重点试验室自主研发的便携式自密封岩石三轴试验高压舱加压系统配合TAW-2000型微机控制电液伺服岩石试验机作为加载系统(图13)，采用匹配型高压舱引伸计通过变形控制以控制岩石试验的破坏，高压舱加载系统与试验机连接方式及引伸计安装如图13所示。便携式自密封岩石三轴试验高压舱加压系统分为高压舱、高精密油压控制系统、三通阀和超高压手泵组成(图14)。系统通过液压油自密封原理，采用液压自密封皮套施加稳定围压，可在短时间内施加高到200 MPa的稳定围压，模拟深部岩体地应力状态。三轴试验中，高压舱加载系统在岩样表面施加径向应力，试验机施加轴向压力。
图13 试验仪器
Fig.13 Test Instruments
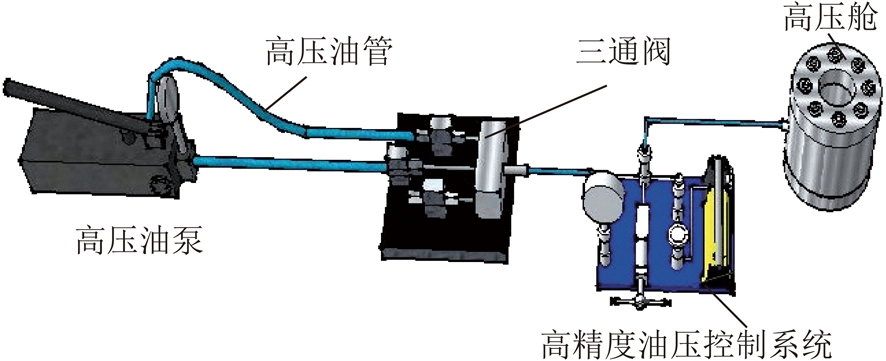
图14 高压舱加载系统
Fig.14 High pressure chamber loading system
图15 三轴压缩试验不同围压下试样破坏
Fig.15 Specimen damage under different confining pressures in triaxial compression test
3.2.2 试验结果分析
四川黄砂岩和金川大理岩部分试样破坏如图15所示。低围压时，试样呈现剪破坏，随着围压的增加，在围压超过90 MPa的两组四川黄砂岩试验中，产生了孔隙坍塌型破坏，为压屈服破坏。由于试验设备不足，没有进行更高压的围压试验，无法观察到完整孔隙坍塌破坏。而金川大理岩由于强度高，未出现孔隙坍塌型破坏。
分别对砂岩和大理岩三轴压缩试验结果进行汇总，计算试样参数，绘制p-q平面中的破坏包络线。理论预测曲线和试验数据比较如图16所示，数据与PMC&BPMC准则吻合度较好。四川黄砂岩在围压达到90 MPa后出现剪应力峰值拐点;低围压时试样呈现剪破坏，随着围压的增加，试件发生压屈服破坏。而金川大理岩在试验中得出的破坏包络线与试验数据拟合度较好。
图16 试样PMC & BPMC破坏包络线与试验数据比较
Fig.16 Comparison of PMC & BPMC failure envelope and test data of specimen
试样破坏强度曲线符合PMC&BPMC模型，该模型能预测孔隙岩石帽子屈服面和破坏模式的过渡，预测岩石不同围压下的破坏模式及其对应的的破坏强度。
(1)考虑多孔岩石孔隙坍塌特征及岩石破坏模式的转化，基于PMC基本原理，提出了高应力下表征压剪屈服BPMC模型。
(2)推导了BPMC公式的摩擦角包络线表示方法，并提供了参数的获取方法。
(3)基于BPMC理论指导对四川黄砂岩和金川大理岩进行高压加载试验，试验结果表明随着围压的增长，破坏模式呈现过渡型特征，且围压在90 MPa后四川黄砂岩出现剪应力峰值拐点。
(4)试验结果证明,PMC&BPMC模型能预测孔隙岩石帽子屈服面和破坏模式的过渡，预测岩石不同围压下的破坏模式及对应的的破坏强度，较好的实际应用意义。
[1] B G TARASOV M R.Frictionless shear at great depth and other paradoxes of hard rocks[J].International Journal of Rock Mechanics and Mining,2008,45(3):316-328.
[2] 昝月稳,俞茂宏.岩石广义非线性统一强度理论[J].西南交通大学报,2013,48(4):616-624.
ZAN Yuewen,YU Maohong.Generalized Nonlinear Unified Strength Theory of Rock[J].Journal of Southwest Jiaotong University,2013,48(4):616-624.
[3] SERRANO A,OLALLA C,REIG I.Convergence of circular tunnels in elastoplastic rock masses with non-linear failure criteria and non-associated flow laws[J].International Journal of Rock Mechanics and Mining Sciences,2011,48(6):878-887.
[4] 尤明庆.统一强度理论应用于岩石的讨论[J].岩石力学与工程报,2013,32(2):258-265.
YOU Mingqing.Discussion on unified strength theories for rocks[J].Chinese Journal of Rock Mechanics and Engineering,2013,32(2):258-265.
[5] SINGH M,SINGH B.Modified Mohr-Coulomb criterion for non-linear triaxial and polyaxial strength of jointed rocks[J].International Journal of Rock Mechanics and Mining Sciences,2012,51:43-52.
[6] HOLCOMB D,RUDNICKI J W,Issen KA & STERNLOF K.Compaction localization in the earth and the laboratory:state of research and research directions[J].Acta Geotech,2007,2(a):1-15.
[7] MEYER J P,LABUZ J F.Linear failure criteria with three principal stresses[J].International Journal of Rock Mechanics and Mining Sciences,2013,60:180-187.
[8] MAKHNENKO R,LABUZ J.Plane strain testing with passive restraint[J].Rock Mechanics and Rock Engineering,2014,47(6):2021-2029.
[9] JOSEPH F Labuz,FEITAO Zeng,ROMAN Makhnenko,et al.Brittle failure of rock:A review and general linear criterion[J].Journal of Structural Geology,2018,112:7-28.
[10] LABUZ J F,DRESCHER A.Bifurcations and instabilities in Geomechanics[M].Minneapolis,Minnesota,Iwbi,2002,2002:29-39.
[11] BAXEVANIS T,PAPAMICHOS E,FLORNES O,et al.Compaction bands and induced permeability reduction in Tuffeaude Masstricht calcarenite[J].Acta Geotech,2006,1(2):123-135.
[12] ISSEN K A.The influence of constitutive models on localization conditions for porous rock[J].Engineering Fracture Mechanics,2002,69(17):1891-1906.
[13] HOLCOMB D,RUDNICKI J W,ISSEN K A,et al.Compaction localization in the earth and the laboratory:State of research and research directions[J].Acta Geotech,2007,2(1):1-15.
[14] ALI Tarokh,YUAN Li.Hardening in porous chalk from precompaction[J].Acta Geotechnica,2017,12(4):949-953.
[15] FEITAO Zeng,YUAN Li,JOSEPH F.Labuz.Paul-Mohr-Coulomb failure criterion for geomaterials[J].Journal of Geotechnical and Geoenvironmental Engineering,2018,144(2):06017018.