
近年由于矿山尾矿的不当堆存与处置,已经引发了多起尾矿库溃坝事故[1-3],造成了严重的环境破坏与人员伤亡。充填采矿法作为一种能够有效消纳矿山尾矿、充填处置采空区,提高资源回收率、合理管控地压的采矿方法,目前已被越来越多的矿山采用。
矿山充填工艺包括充填料浆制备、输送与采空区充填3个关键步骤。而在料浆制备过程中,充填尾砂首先需要经过沉降脱水与浓密过程,得到具有一定浓度的底流后,再通过搅拌与其他物料充分混合,从而获得设计配比的充填料浆[4]。因此,尾砂浓密效果的优劣将直接影响最终充填料浆的质量。目前,国内对于充填尾砂浓密过程的研究仍以室内沉降实验为主,即直接通过尾砂沉降实验,测试不同初始浓度的尾砂浆经沉降后的底流浓度,从而建立相关经验计算公式[5-6]。例如,焦华哲等利用全尾砂的絮凝沉降实验,观察得到了充填尾砂的“分层沉降”结论[7]。李辉等[8]利用深锥浓密机相似模型,通过观察充填尾砂在模型中的动态絮凝沉降过程,探索了入料浓度、絮凝剂单耗等参数对于该过程的影响。上述研究对于指导工程实践具有非常重要的意义,但对于尾砂颗粒沉降过程的内在沉降速率变化机理则较少涉及,制约了科学数学描述充填尾砂浓密过程,不利于矿山充填精确化控制。
因此,笔者将以国内外现有的干扰沉降理论为指导,通过充填尾砂沉降实验,探索并论证相关理论在充填领域的适用性,为下一步充填尾砂沉降、固结与浓密过程的整体建模研究奠定基础。
充填尾砂在其沉降过程中,尾砂颗粒与颗粒之间将发生碰撞、摩擦等相互作用,对此,需要利用“干扰沉降”的相关理论进行研究[9-10]。对于“干扰沉降”,首先提出定量化研究理论的是KYNCH等[11]。通过假设干扰沉降颗粒平均沉降速率与其体积浓度相关,基于物料质量守恒,KYNCH[11]提出:
(1)
fbk(Φ)=Φu(Φ)
(2)
其中,z为沉降高度,m;t为沉降时间,s;Ф为颗粒体积浓度;fbk(Ф)为颗粒通量;u为颗粒沉降速率,m/s。利用式(1)和(2),若以Ф为控制变量,求解偏微分方程,则需要找到u与Ф的本构关系。
沉降颗粒自身可能存在的级配与比重的差异,干扰沉降因此可进一步分为“均匀干扰沉降”与“非均匀干扰沉降”。对于“均匀干扰沉降”,研究人员分别提出了多种经验、半经验计算模型。如Richardson-Zaki理论[12]、Batchelor理论[13]、Barnea-Mizrahi理论[14]等。在泥沙颗粒沉降研究中应用较广的为Richardson-Zaki计算模型[12]:
fbk(Φ)=u Φ(1-Φ)n,n>1
Φ(1-Φ)n,n>1
(3)
其中,u∞为颗粒自然沉降时的沉降末速,m/s;n为与颗粒雷诺数(Re)相关的系数。对不同的雷诺数范围Richardson-Zaki理论也给出了不同的n系数的经验计算公式。
同样地,对于“非均匀干扰沉降”,目前也存在多种相关计算理论。最简单的方式,即不考虑非均匀颗粒间的相互作用,仅按照上述均匀颗粒计算理论计算。除此之外,SELIM等认为非均匀颗粒间相互作用将以较粗颗粒在细颗粒与料浆中液体所形成的“混合溶液”中沉降的形式表征,并由此对Richardson-Zaki理论进行了修正[15]。具体计算:
(4)
![]()
(5)
uL=uL, (1-ΦL-ΦS)n
(1-ΦL-ΦS)n
(6)
式中,uL,∞为修正后的粗颗粒自由沉降末速,m/s;uL为粗颗粒非均匀干扰沉降速率,m/s;ρL为粗颗粒密度,kg/m3;ρp为细颗粒与料浆中液体所构成混合溶液的密度,kg/m3;ρf为料浆中液体的密度,kg/m3;ρS为细颗粒密度,kg/m3;ФL与ФS分别为料浆中粗颗粒与细颗粒的体积分数;dL为粗颗粒粒径,m;μf为料浆中液体的表观黏度系数,Pa·s。
除此之外,应用较广的还包括Smith理论[16]、Masliyah计算模型[17]等经验半经验公式。
本研究将通过室内充填尾砂沉降实验,获得尾砂沉降速率,对比讨论了Richardson-Zaki“均匀干扰沉降”计算模型以及Selim“非均匀干扰沉降”计算模型在计算充填尾砂干扰沉降过程时的可行性。
取某矿山全尾砂,经水力旋流分级后,分别获得分级尾砂与溢流细砂作为实验物料。依照相关测试标准(GB/T 50123—1999[18]及JTG E42—2005[19])测试分级尾砂与溢流细砂的基本物理性质见表1。
表1 尾砂基本物理性能
Table 1 Basic physical properties of tailings

类别颗粒密度/(t·m-3)堆积密度/(t·m-3)堆积空隙率/%分级尾砂2.921.6047.58溢流细砂2.870.8173.52
由于尾砂较细,使用激光粒度测试方法分别对分级尾砂与溢流细砂的粒径分布进行测试。测试结果见表2。
表2 尾砂粒度分布
Table 2 Particle size distribution of tailings

粒径范围/μm分级尾砂/%溢流细砂/%-109.7631.9-2027.454.4-4049.785.1-5054.592.1-7470.997.3-10088.299.6-15099.499.9-20099.999.9
经测试,分级尾砂的体积平均粒径约为40 μm,而溢流细砂的体积平均粒径约为20 μm。两种尾砂的孔隙率、粒径分布均差异明显,是进行本次实验研究较为理想的物料。
实验分为“均匀干扰沉降”实验以及“非均匀干扰沉降”探索实验两部分。对于“均匀干扰沉降”实验,采用分级尾砂作为实验物料。尽管分级尾砂中仍然存在一定程度的颗粒粒径差异,但分级处理是矿山尾砂处理的常用方法,以分级处理过后的尾砂作为实验原料探索其沉降过程能否以“均匀干扰沉降”理论来分析仍具有非常重要的实践意义。同样的,对于“非均匀干扰沉降”实验,利用在分级尾砂中添加溢流细砂的形式,获得具有不同粒径与比重的混合物料作为实验物料。论证现有理论对混合物料中分级尾砂与溢流细砂间相互作用的“非均匀干扰沉降”的适用性,具有直观的实践指导意义。
2.2.1 分级尾砂均匀干扰沉降实验
(1)以1 L标准量筒为实验容器。量筒一侧贴上刻度标签用以观察记录尾砂浆沉降过程中的液面高度。
(2)以分级尾砂为原料,分别按照60%,63%,65%,70%质量分数配置800 mL尾砂浆。为排除水中离子的影响,试验用水均为蒸馏水。
(3)将配置尾砂浆倒入量筒,用带网孔搅拌棒充分搅拌,然后静置,并于不同时间点观察记录在1 h内料浆液面的沉降高度。
2.2.2 充填尾砂非均匀干扰沉降实验
(1)添加质量分数(占总物料质量)为15%的溢流细砂,与分级尾砂充分混合搅拌,作为“非均匀干扰沉降”实验用物料。
(2)按照上述相同的实验步骤,分别配置60%,63%,65%,70%质量分数的尾砂浆进行沉降实验,记录相应液面沉降高度。
分别对不同尾砂浆沉降数据进行拟合分析,得到相应的沉降曲线,如图1,2所示。

图1 分级尾砂均匀干扰沉降过程沉降曲线
Fig.1 Settlement curves of hindered settling processes of classified tailings

图2 分级尾砂与15%溢流细砂“非均匀干扰沉降”过程沉降曲线
Fig.2 Polydisperse settling curves of tailings slurry containing 15% fine tailings
为分析充填尾砂颗粒的沉降速率,对上述干扰沉降曲线进行高次多项式拟合,并保证拟合优度R2大于0.95。按照KYNCH理论假设[7],认为沉降曲线上各点的斜率表征了该点所在时刻的沉降速率值。因此可对上述拟合多项式进行求导,其导函数值即为不同时间点的颗粒沉降速率值。同时为排除料浆受搅动作用引起的初始紊流的影响,选取沉降3 min后的稳定数值作为参考值。拟合曲线示意图如图3所示。
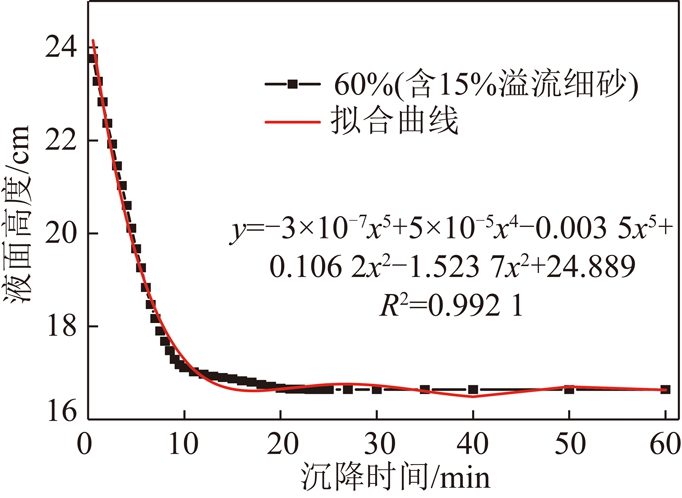
图3 含15%溢流细砂60%质量分数尾砂浆的沉降曲线拟合结果
Fig.3 Fitting curves of the 60% tailings slurry containing 15% fine tailings
不同配比尾砂浆干扰沉降速率拟合值见表3。
表3 沉降速率拟合方程计算结果
Table 3 Calculated results of the fitted settling curves
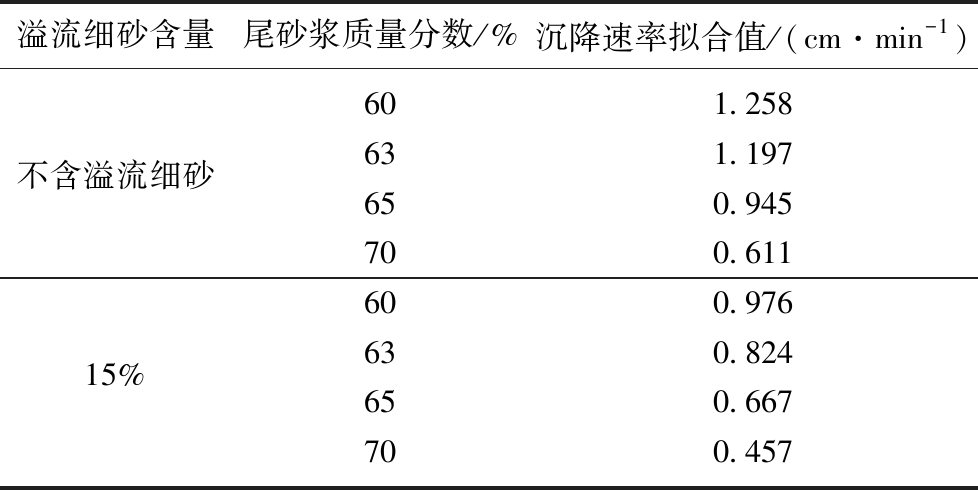
溢流细砂含量尾砂浆质量分数/%沉降速率拟合值/(cm·min-1)601.258631.197不含溢流细砂650.945700.611600.976630.82415%650.667700.457
按照Richardson-Zaki理论对分级尾砂均匀干扰沉降数据进行理论计算[12]:
u=u Φ(1-Φ)n
Φ(1-Φ)n
(7)
u∞按Stockes颗粒自由沉降速率模型计算[20]:
u
![]()
(8)
其中,ρ为颗粒密度,kg/m3;d为颗粒粒径,m。分级尾砂粒径取其体积平均粒径40 μm进行计算,代入式(8),经计算u∞=1.67×10-3m/s。将其代入式(9)计算颗粒雷诺数:
Re=dvρf/μf
(9)
其中,v为颗粒沉降速率,此处为u∞,m/s。经计算,颗粒雷诺数Re<0.2,此时系数n[12]为
(10)
其中,D为容器直径,m。经计算,n取4.66,因此对于该分级尾砂,其Richardson-Zaki计算公式为
u=1.67×10-3×(1-Φ)4.66
(11)
将沉降实验中尾砂浆的质量分数分别代入上述理论计算公式进行计算,并对比分析了理论值与实验拟合值曲线,如图4所示。由图4可知,4组实测数据分别分布于Richardson-Zaki理论曲线两侧,且实测值与理论计算值间差异不大。

图4 分级尾砂均匀干扰沉降速率实验值与理论值对比
Fig.4 Comparison of experimental and theoretical hindered settling rate of graded tailings
根据残差分析相关理论,分别计算实验值相对于理论计算值的残差,其结果见表4,并绘制残差分布图,如图5所示。由图5可知,体积分数36.83%(对应质量分数63%)料浆的实测沉降速率值大于理论计算值,其他3组料浆实验值则小于理论计算值。由此可以判断分级尾砂体积分数与残差值之间不存在显著规律性。
其次,通过计算4组实测数据与理论值间的相关性可决系数,所得结果为R2≈0.87,也说明计算值与实验值之间存在较为显著的相关性。因此,可初步说明采用Richardson-Zaki理论计算模型计算该充填尾砂的“均匀干扰沉降”过程具有可行性。
表4 分级尾砂均匀干扰沉降速率残差值
Table 4 Residual values of hindered settling rate of graded tailings

分级尾砂体积分数/%实测值/(cm·min-1)理论计算值/(cm·min-1)残差值/(cm·min-1)33.941.2581.454-0.19636.831.1971.1800.01738.880.9451.012-0.06744.420.6110.650-0.039

图5 Richardson模型计算结果相对沉降速率实测值的残差分布
Fig.5 Residual error map of hindered settling rate between Richardson method results and measured values
基于该理论的假设[12],可认为对于尾砂颗粒均匀干扰沉降,尽管从微观上看两两颗粒间的相互作用方式无法获得,但从大量颗粒的相互作用对于颗粒沉降速率的影响角度分析,其平均沉降速率仍然只与颗粒在料浆中的体积分数有关,即沉降速率仍只是其体积分数的函数。
同时,实测值与理论值间的可决系数仍未超过0.9,可能是由于该计算过程采用分级尾砂平均体积粒径,而未能充分考虑到颗粒级配对其干扰沉降的影响有关。因此,仍有必要进一步研究充填尾砂的“级配”对其“干扰沉降”过程的影响。
对于“非均匀干扰沉降”,由于溢流细砂相对分级尾砂其中值粒径较小,选取SELIM计算模型进行分析。并为进一步分析“均匀干扰沉降”与“非均匀干扰沉降”的差异,可假设在添加溢流细砂后,粗细尾砂颗粒不产生相互作用,再次采用Richardson-Zaki理论计算模型对分级尾砂沉降速率进行计算,并以其结果进行对比分析。
将上述分级尾砂与溢流细砂具体物理参数分别带入理论公式,并结合实测数据值,绘制相应对比分析曲线,如图6所示。
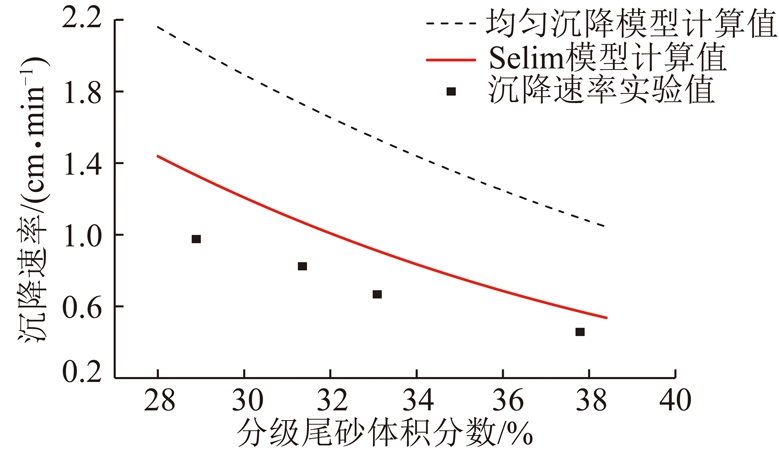
图6 分级尾砂“非均匀干扰沉降”理论值与实测值对比
Fig.6 Comparison diagram of experimental and theoretical polydisperse settling rate of graded tailings
由图6可知,SELIM模型计算结果较“均匀干扰沉降”模型(此处为Richardson-Zaki理论计算模型)计算结果更接近实测值。且SELIM模型计算值与实测值均小于“均匀干扰沉降”模型计算值,这与非均匀干扰沉降过程中粗细颗粒将发生相互作用,从而降低沉降速率的结论相吻合。说明SELIM理论能够表征出尾砂颗粒“非均匀干扰沉降”过程中受粗细颗粒相互作用而导致两类颗粒沉降速率降低的这一特性。
其次,对于SELIM模型计算结果,计算其实测值相对于理论计算值的残差值,并绘制相应分布图,如表5与图7所示。由图7可知,残差值与分级尾砂体积分数间存在规律性关系,即随着体积分数的减小,残差值增大。这与SELIM模型低估了细颗粒对粗颗粒沉降的阻碍作用有关,即在该种尾矿沉降过程中,仅将细颗粒看作阻碍分级尾砂沉降的溶质将低估细颗粒对于粗颗粒的“干扰”作用,从而计算得到了较大的“干扰沉降速率”值。
表5 分级尾砂非均匀干扰沉降速率残差值
Table 5 Residual values of polydisperse settling rate of graded tailings

分级尾砂体积分数/%实测值/(cm·min-1)理论计算值/(cm·min-1)残差值/(cm·min-1)28.890.9761.332-0.35631.350.8241.070-0.24633.090.6670.911-0.24437.790.4570.571-0.114
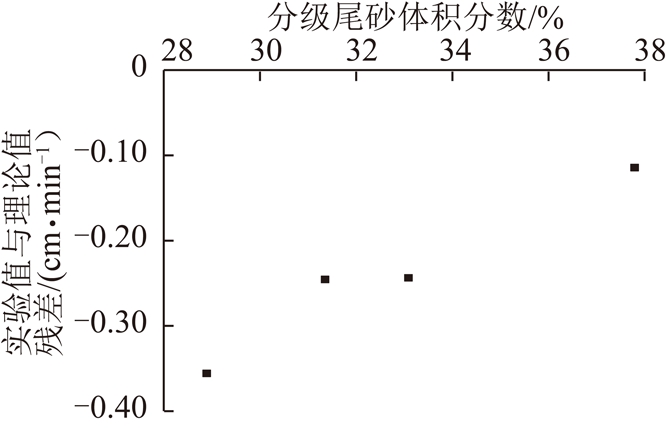
图7 Selim理论计算值相对沉降速率实测值的残差分布
Fig.7 Residual error of polydisperse settling rate between Selim method results and measured values
综上所述,在充填尾砂“非均匀干扰沉降”过程中,忽略不同粒径颗粒间相互作用,仅按照“均匀干扰沉降”模型进行计算,将得到大于实际情况的沉降速率值。因此,不同粒径间颗粒的相互作用方式及其表征方法是研究尾砂颗粒非均匀干扰沉降机理的核心问题。SELIM理论的假设在本次研究中“低估”了细颗粒对粗颗粒的“阻滞作用”。除此之外,MASLIYAH[17]理论假设粗、细颗粒间相互作用将以两种颗粒在其共同组成的“混合溶液”中发生沉降;而Davis-Gecol理论则强调当粗、细颗粒粒径差异非常大时,颗粒间的粒径比将是决定各自沉降速率的关键参数等。对于上述各项理论假设到底分别适用于何种级配特性的尾砂,还需要进行更为系统的专题研究。
(1)在尾砂颗粒均匀干扰沉降过程中,Richardson-Zaki计算模型的计算值与实测值之间的残差经计算无明显规律性,且两者的相关性可决系数达0.87,其相关性较为显著,能够对实际尾砂颗粒的均匀干扰沉降速率进行计算。
(2)对尾砂颗粒的非均匀干扰沉降,粗细颗粒间的相互作用将对颗粒的沉降起到显著阻碍作用。相较于Richardson-Zaki计算模型,SELIM计算模型能够有效反映上述阻碍作用,其计算值较为准确,但仍需要进一步研究细颗粒粒径级配的影响性。
(3)基于不同理论模型的充填尾砂颗粒干扰沉降实验结论能够为充填尾砂浓密过程的理论研究与工程实践提供参考。下一步将对尾砂级配对干扰沉降的影响以及粗细颗粒相互作用的定量描述等问题进行深入研究。
[1] 杨小聪,郭利杰,许文远,等.尾矿和废石综合利用技术[M].北京:化学工业出版社,2018:1-3.
[2] 尹光志,敬小非,魏作安,等.尾矿坝溃坝相似模拟试验研究[J].岩石力学与工程学报,2010,29(S2):3830-3838.
YIN Guangzhi,JING Xiaofei,WEI Zuoan,et al.Experimental study of similar simulation of tailings dam-break[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(S2):3830-3838.
[3] 梅国栋,吴宗之.尾矿库溃坝风险定量评价方法探讨[J].中国安全生产科学技术,2012,8(2):78-82.
MEI Guodong,WU Zongzhi.Discussion on quantitative assessment method of dam failure risks in tailings dam[J].Journal of Safety Science and Technology,2012,8(2):78-82.
[4] 黄玉诚.矿山充填理论与技术[M].北京:冶金工业出版社,2014:7-9.
[5] 史秀志,胡海燕,杜向红,等.立式砂仓尾砂浆液絮凝沉降试验研究[J].矿冶工程,2010,30(3):1-3.
SHI Xiuzhi,HU Haiyan,DU Xianghong,et al.Experimental study on flocculating sedimentation of tailings slurry in a vertical sand tank[J].Mining and Metallurgical Engineering,2010,30(3):1-3.
[6] 王洪江,王勇,吴爱祥,等.细粒全尾动态压密与静态压密机理[J].工程科学学报,2013,35(5):566-571.
WANG Hongjiang,WANG Yong,WU Aixiang,et al.Dynamic compaction and static compaction mechanism of fine unclassified tailings[J].Chinese Journal of Engineering,2013,35(5):566-571.
[7] 焦华喆,王洪江,吴爱祥,等.全尾砂絮凝沉降规律及其机理[J].工程科学学报,2010,32(6):702-707.
JIAO Huazhe,WANG Hongjiang,WU Aixiang,et al.Rule and mechanism of flocculation sedimentation of unclassified tailings[J].Chinese Journal of Engineering,2010,32(6):702-707.
[8] 李辉,王洪江,吴爱祥,等.基于尾砂沉降与流变特性的深锥浓密机压耙分析[J].北京科技大学学报,2013,35(12):1553-1558.
LI Hui,WANG Hongjiang,WU Aixiang,et al.Pressure rake analysis of deep cone thickeners based on tailings’ settlement and rheological characteristics[J].Journal of University of Science and Technology Beijing,2013,35(12):1553-1558.
[9] 郭亚兵,胡钰贤,王守信.沉降-浓缩理论及数学模型[M].北京:化学工业出版社,2014:9-10.
[10] BUSTOS M C,TORY E M,BÜRGER,et al.Sedimentation and thickening:Phenomenological foundation and mathematical theory (Vol.8)[M].New York:Springer Science and Business Media,1999:27-29.
[11] KYNCH G J.A theory of sedimentation[J].Transactions of the Faraday Society,1952,48(2):166-176.
[12] RICHARDSON J F,ZAKI W N.Sedimentation and fluidization:Part I[J].Transactions of the Institution of Chemical Engineers.1954,32:35-53.
[13] BATCHELOR G K.Sedimentation in a dilute dispersion of spheres[J].Journal of Fluid Mechanics,1972,52(2):245-268.
[14] BARNEA E,MIZRAHI J.A generalized approach to the fluid dynamics of particulate systems:Part 1.General correlation for fluidization and sedimentation in solid multiparticle systems[J].Chemical Engineering Journal,1973,5(2):171-189.
[15] SELIM M S,KOTHARI A C,TURIAN R M.Sedimentation of multisized particles in concentrated suspensions[J].AIChE Journal,1983,29(6):1029-1038.
[16] SMITH T N.Differential sedimentation of particles of two different species[J].Transactions of the Institution of Chemical Engineer,1965,43(3):69-73.
[17] MASLIYAH J H.Hindered settling in a multi-species particles system[J].Chemical Engineering Science,1979,34(9):1166-1168.
[18] GB/T 50123—1999,土工试验方法标[S].
[19] JTG E42—2005,公路工程集料试验规程[S].
[20] HAPPEL J,BRENNER H.Low Reynolds number hydrodynamics:With special applications to particulate media[M].New York:Springer Science and Business Media,2012:3-10.