移动阅读
移动阅读
钻孔密封性已经成为制约煤矿井下瓦斯抽采和利用的主要因素之一。特别是对于煤质松软及煤体结构破碎的煤层，在瓦斯饱和度及含量较低的情况下，钻孔抽采瓦斯体积分数低的状况尤为突出，初始抽采体积分数通常低于10%～30%，瓦斯抽采效率受到极大的制约并造成瓦斯资源的巨大浪费[1]。
大量的现场试验表明，钻孔密封工艺对煤层具有明显的条件适用性。例如，即使采用相同的 “两堵一注” 膨胀水泥带压封孔工艺，在不同矿井，同一矿井的不同区域和不同构造程度煤层中，钻孔密封效果的分区现象十分明显，抽采瓦斯体积分数通常会在5%～60%较大范围内波动，且平均抽采瓦斯体积分数衰减速度较快，造成严重的瓦斯输送和利用困难。前人研究结果表明[2-3]，钻孔抽采瓦斯体积分数的偏低，主要是由于钻孔密封段围岩裂隙、密封材料自身结构及二者之间存在漏气空隙等因素所致。目前钻孔密封主要采用以膨胀水泥为主的“两堵一注”封孔工艺[4]，属主动式带压封孔。在钻孔理论密封半径参数的选择上，一般通过求解理想弹塑性模型Kastner方程的塑性区半径来获得[5-6]。事实上，煤层是一种弱结构非常发育的弹塑性材料，在采动过程中表现出明显的塑性软化及扩容特征[7-8]。而对于弱结构煤层而言，这一现象更为突出。近年来，随着对软岩巷道研究的不断深入，陈进[9]、付国彬[10]、范文[11]及姚国圣等[12-13]一致认为软岩的塑性软化及扩容特性对巷道的塑性半径及径向位移具有不可忽略的作用，考虑岩体塑性软化及扩容特性后计算的巷道围岩塑性区半径及径向位移均大于Kastner解，说明利用理想弹塑性Kastner模型求解弱结构煤岩塑性区半径并不合理;郝富昌等[14-15]通过研究抽放钻孔流变规律，发现软煤具有明显的塑性软化、扩容及流变特征，钻孔蠕变缩径的现象更加明显。此外，钻孔围岩塑性扩容是内生裂隙增生、扩展、贯通而产生的结果[16]，钻孔围岩径向位移越大，塑性区裂隙发育程度越高，漏气越严重，导致瓦斯抽采浓度也越低。因此，准确认识煤岩的塑性软化及扩容特性，从而合理计算钻孔围岩塑性流动扩容区半径及径向位移，对钻孔注浆密封参数设计和新型密封材料开发，均具有重要的意义。
煤岩体是一种典型的弱结构面非常发育的弹塑性材料，结构面的存在使得煤体在加载过程中具有典型的应力软化及扩容特性。由于钻孔平面及力学性质具有对称特征，可根据钻孔围岩不同采动区域的性质，将钻孔围岩由内而外分为弹性区、塑性软化区及塑性流动区。围岩的平面力学模型如图1所示。
图1 煤层钻孔力学模型
Fig.1 Borehole mechanics model of coal seam
图1中，p0为原岩应力;R0为钻孔半径;Rp为塑性软化区半径;Rb为塑性流动区半径;r0为钻孔封孔前实际半径;u0为钻孔围岩位移;R为钻孔围岩理论密封半径。
通过对煤层取样并对其力学性质进行测试，可得到煤体的全应力应变曲线。同时，为了更好地研究钻孔围岩的软化及扩容特征，本文采用应力应变软化三线段曲线模型对全应力应变曲线及环向应变-轴向应变曲线进行简化，如图2所示。
图2 煤体力学特性曲线及简化三线段曲线模型
Fig.2 Mechanical characteristic curves of coal and simplified three lines model
图2中，σ1，σ3为最大、小主应力;ε1，ε3为最大、最小主应变;
和
分别为塑性软化区和塑性流动区在坐标轴中的对应应变量;
为弹性区在坐标中的对应应变量;k为软化系数，k=M0=tan α，α为软化角[17];η1,η2为扩容系数。
(1)极坐标系下的基本方程(忽略体力[18])
平衡方程:
(1)
几何方程:
(2)
式中，σr和σθ分别为煤层钻孔径向和切向应力，分别对应图2中σ3和σ1;εr，εθ为钻孔围岩径向和切向应变，分别对应图2中ε3，ε1;u为钻孔围岩径向位移。
(2)屈服准则
煤体屈服准则采用线性Mohr-Coulomb屈服准则，表达式[19]如下:
σθ=Kpσr+σc
(3)
式中，Kp(φ)为煤体强度系数，Kp=(1+sin φ)/(1-sin φ);σc(φ,c)为煤体峰值强度，
为煤体内摩擦角;c为煤体黏聚力。
因此，在塑性软化区有:
(4)
在塑性流动区有:
(5)
式中，
和
分别为塑性软化区和塑性流动区切向应力和径向应力;
和
为煤体塑性软化区内摩擦角及黏聚力，其中
和Mc为塑性软化区内摩擦角和黏聚力软化模量，且有
和c0,φr,cr分别为煤体峰值和塑性流动区内摩擦角和黏聚
为单轴抗压残余强度。令图2模型曲线中σ3=0，由理想塑性软化模型可得
(6)
式(6)中，可令M0=Mc。
(3)塑性流动法则
根据图2(b)，考虑煤体体积扩容的流动法则可得:
塑性软化区:
(7)
塑性流动区：
(8)
式中，
和
分别为塑性软化区和塑性流动区的径向和切向应变增量;当考虑扩容时，η1>1,η2>1;否则，η1=1，η2=1，且有
根据文献[10]，η2一般可取1.30～1.50。
1.4.1 煤层钻孔围岩弹塑性位移解
(1)弹性区位移解
根据弹性理论知识可得弹性区钻孔围岩径向应力
切向应力
和径向位移ue[21]为
(9)
(10)
(11)
(12)
式中，ν为煤岩泊松比;E为煤岩弹性模量;σRp为r=Rp处的径向应力;A为相关系数，且A=(1+ν)(p0-σRp)/E。
(2)塑性软化区位移解
根据图2(b)可得出，在塑性软化区内，径向应变εr和切向应变εθ可写成
(13)
则由式(2)，(7)和(13)可得软化区的位移为
(14)
联立式(13)和式(1)可得
(15)
在弹塑性交界处，有
(16)
联立式(4)，(15)和(16)可得
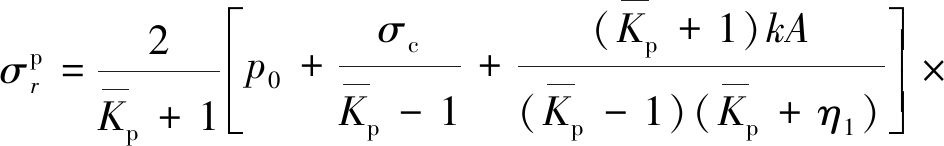
(17)
(3)塑性流动区位移解
根据图2(b)在塑性流动区内，径向应变εr和切向应变εθ可写成
(18)
由式(2)，(8)和(18)可得流动区径向位移ub为
(19)
因此，可得煤层钻孔围岩位移u0的解析表达式为
(20)
在塑性软化区和流动区交接处有
(21)
联立式(1)，(5)和(21)可得
(22)
可联立式(8)和式(22)解得。
1.4.2 煤层钻孔围岩塑性区半径解
煤层钻孔围岩塑性区半径主要包括塑性软化区Rp和塑性流动区Rb。
(1)当钻孔围岩处于塑性状态时，有
代入式(17)可得
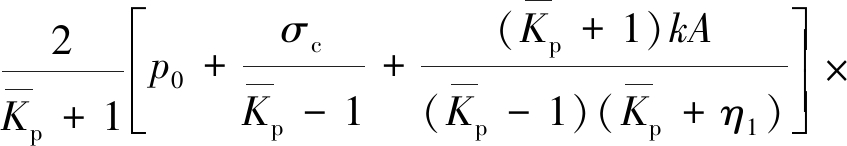
(23)
(2)当钻孔围岩处于塑性流动状态时，有
或者
联立式(6)，(20)可得
(24)
且当
代入式(22)可得流动区半径为
(25)
(3)当钻孔围岩处于临界塑性流动状态时，则由Rb=R0，可得塑性软化区半径为
(26)
钻孔围岩理论密封半径R是指在实施带压注浆钻孔密封过程中，密封浆液在钻孔周围煤体内理论上所应渗透的径向距离。由于钻孔密封的主要目标是对采动塑性破坏等产生的钻孔围岩裂隙进行充填，因此，钻孔围岩理论密封半径R主要由钻孔围岩软化区半径Rp、塑性流动区Rb径向位移半径u0的差值构成。其中钻孔围岩软化区半径Rp与径向位移半径u0的差值构成R的最大值;而塑性流动区Rb与径向位移半径u0的差值则构成R的最小值。下文中所计算的钻孔围岩理论密封半径主要指R的最大值。因此有:
(1)当η1=1,η2=1，k=0时。代入式(14)，(23)，可得理论钻孔围岩密封半径R0为
(27)
式中，R1为在不考虑煤体塑性软化和扩容条件时由Kastner方程所获得的钻孔围岩理论密封半径。
(2)当η1>1，η2>1，k=0时。代入式(20)，(24)，(25)，可得钻孔围岩理论密封半径R2为
(29)
(30)
式中，R2为仅考虑煤体塑性软化而不考虑扩容所获得的钻孔围岩理论密封半径。
(3)当同时考虑煤层应力软化及扩容特性时，即η1>1，η2>1，k>0时。由式(20)，(24)，(25)可得钻孔围岩理论密封半径R3为
R3=Rp+u0-R0
(32)
本文以山西高河能源有限公司3号煤层为例，煤样采集地点为W3305运输巷(里程1 218 m处)，该区域煤层受附近小构造影响，平均坚固性系数f为0.6，但煤体完整性相对较好。煤样的主要力学参数为:p0=19.22 MPa，E=2 278 MPa，σc=12.19 
mm，η2=1.4，k=1。将各参数代入式(27)～(32)可得各条件下钻孔围岩理论密封半径，见表1。
表1 不同条件下煤层钻孔围岩理论密封半径解
Table 1 Grouting radius solution of surrounding borehole in coal seam under different conditions mm
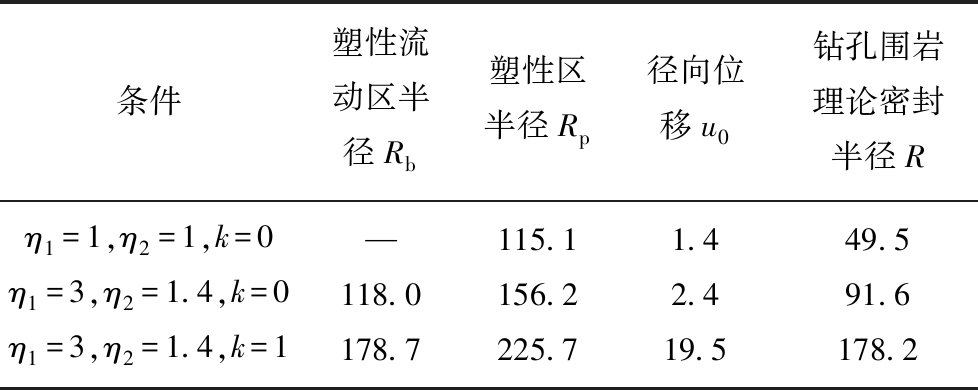
条件塑性流动区半径Rb塑性区半径Rp径向位移u0钻孔围岩理论密封半径Rη1=1,η2=1,k=0—115.11.449.5η1=3,η2=1.4,k=0118.0156.22.491.6η1=3,η2=1.4,k=1178.7225.719.5178.2
由表1可知，与仅考虑煤体的塑性破坏的经典KASTER解相比，考虑煤体的塑性软化特征得到的塑性区半径Rp增加了35.71%，径向位移从1.4 mm增加到2.4 mm，钻孔围岩密封半径的理论值提高了0.85倍。因此，仅考虑煤体的软化特性时，塑性区半径的增加幅度较大，而径向位移增加的幅度则相对较小;而由式(27)和(30)第2式可知，密封半径R的增加主要是由塑性区半径增加所引起的。
当同时考虑煤体的塑性软化和扩容效应时，钻孔围岩塑性区半径Rp与不考虑该条件相比增加96.09%，与仅考虑煤体塑性软化条件相比增加44.49%，径向位移u分别提高了12.93倍和7.13倍，这表明煤岩塑性软化及扩容特性是造成钻孔围岩径向位移的主要原因之一;且钻孔围岩理论密封半径R也同比增加2.60倍和0.95倍，其主要原因是由于钻孔围岩煤体受采动扩容效应使得塑性流动区半径和钻孔径向位移增加所致。因此，在塑性软化及扩容特性的影响作用下，利用经典理想弹塑性模型(Kastner)解来确定钻孔围岩所需注浆参数及注浆渗透半径是不合理的。
山西高河能源有限公司3号煤层属高瓦斯煤层，受小构造影响，在掘进过程中相邻区域的煤层力学性质出现明显差异，初始抽采瓦斯体积分数也出现明显的波动。为进一步研究密封前钻孔围岩特征对钻孔密封性的影响作用，利用ZKXG100矿用钻孔成像轨迹装置分别3号煤层W3305运输巷1 521 m处右侧顺层118-1号钻孔及过小构造区121-3号钻孔相邻区域两组钻孔进行成像对比。该区域煤层坚固性系数平均0.45，平均瓦斯含量为11.06 m3/t，瓦斯压力0.68 MPa，煤体瓦斯组分中，甲烷体积分数为91%～93%;钻孔内部结构对比结果如图3所示。
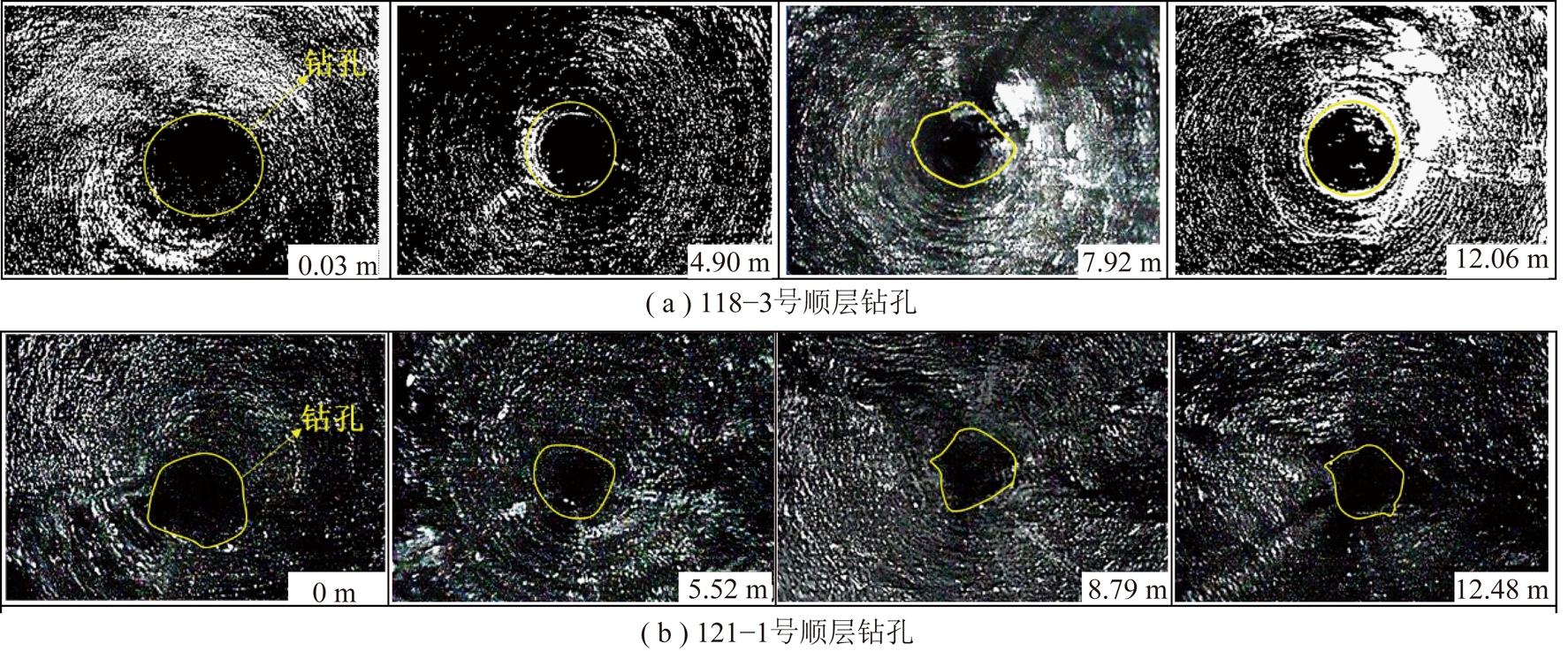
图3 钻孔内部特征
Fig.3 Internal characteristics of boreholes
如图3可知，与非构造区相比，小构造区域121-1号顺层钻孔由于受地质构造作用影响，煤体强度及结构发生明显变化，钻孔围岩表现出更为明显的扩容特性，具有明显的缩径现象。而非构造区顺层118-3号钻孔围岩虽然有一定的变形，但缩径变形量较118-3号钻孔相比相对较小。由3.2节计算结果可知，钻孔缩径越严重，钻孔围岩所需密封的理论半径越大;同理，钻孔围岩理论密封半径越大，即钻孔围岩体积扩容量越大，漏气裂隙半径也随之增大。
钻孔抽采瓦斯体积分数是钻孔密封性评价的重要指标之一。为对比分析煤体塑性软化及软化特征对钻孔密封性的影响作用，对上述118号和121号两组顺层组孔采用相同的“两堵一注” 密封工艺，每组密封钻孔6个。钻孔密封参数见表2。
表2 钻孔密封参数
Table 2 Borehole sealing parameters
项目名称始封深度/m封孔段长度/m水灰比注浆压力/MPa水泥膨胀率/%参数值1.8141∶1.31>25
密封完成后，使用CJZ4Z钻孔瓦斯抽采综合参数测定仪对各组钻孔抽采数据进行采集，采集周期为29 d，各组采集数据统计分析如图4所示。
图4 各组实验孔平均抽采瓦斯体积分数分布
Fig.4 Distribution of the average gas concentration in each experimental borehole
由图4可以看出，在水泥浆液完全充填钻孔的情况下，两组钻孔初始抽采瓦斯体积分数均小于煤层原始瓦斯体积分数，这表明水泥浆液并未完全封闭钻孔围岩裂隙，进而导致抽采瓦斯体积分数降低。同时，结合图3和4可看出，对于缩径现象较为明显的121号组钻孔，抽采瓦斯浓度在初始阶段均小于非构造区域118号组钻孔。121号和118号组钻孔在初始一周内平均抽采体积分数分别为24.39%和59.00%，同比降低59.00%;且在29 d考察期内平均抽采体积分数分别为19.23% 和54.83%，同比降低64.92%;且各组钻孔瓦斯体积分数衰减率分别为21.16%和7.07%，同比增加3倍。说明受塑性软化及扩容特性的影响，钻孔围岩裂隙的发育程度和理论密封半径均大大增加，进而导致更多漏气裂隙通道的形成，钻孔抽采瓦斯体积分数后期衰减也更快。因此，对钻孔密封过程中的注浆压力、浆液渗透半径、钻孔密封长度等参数的设计，以及所注浆液的渗透性及胶结性等性能要求应根据煤层变化进行确定，特别是受塑性软化及扩容特性影响较大的煤层，与采动变形较小的煤层采用同一种钻孔密封参数并不合理。
(1)通过构建煤岩线弹塑性力学软化模型，推导了煤岩塑性软化及扩容特性影响下的钻孔围岩弹塑性半径、径向位移及理论密封半径解析解;得出钻孔围岩理论密封半径应采用公式:R=Rp+u0-R0来计算;研究结果为钻孔密封长度、注浆压力及渗透半径等参数的设计，密封材料的开发提供借鉴。
(2)同仅考虑煤体塑性破坏的经典Kastner解相比较，考虑煤体的塑性软化及扩容特性后，钻孔围岩塑性区半径Rp同比增加了96.09%，径向位移u提高了12.93倍，钻孔围岩理论密封半径增加2.60倍，充分证明利用Kastner解求得的煤层钻孔围岩理论渗透半径和注浆压力等参数的不合理性。
(3)受煤体塑性软化及扩容特性影响，钻孔围岩缩径明显，且相同密封工艺条件下，与相邻缩径量较小的钻孔相比，单孔平均抽采瓦斯体积分数同比降低64.92%，瓦斯体积分数衰减率增加3倍;因此，钻孔密封参数应根据煤层特性进行区别选择。
[1] 吴立新,赵路正.煤矿区煤层气开发利用制约因素与发展建议[J].洁净煤技术,2014,20(5):24-27,52.
WU Lixin,ZHAO Luzheng.Restrictive factors and development suggestions of coalbed methane extraction and utilization[J].Clean Coal Technology,2014,20(5):24-27,52.
[2] 周福宝,孙玉宁,李海鉴,等.煤层瓦斯抽采钻孔密封理论模型与工程技术研究[J].中国矿业大学学报,2016,45(3):433-439.
ZHOU Fubao,SUN Yuning,LI Haijian,et al.Research on the theoretical model and engineering technology of the coal seam gas drainage hole sealing[J].Journal of China University of Mining & Technology,2016,45(3):433-439.
[3] 王志明,孙玉宁,王永龙,等.瓦斯抽采钻孔动态漏气圈特性及漏气处置研究[J].中国安全生产科学技术,2016,12(5):139-145.
WANG Zhiming,SUN Yuning,WANG Yonglong,et al.Study on characteristics of dynamic leakage ring and leakage disposal of gas extraction borehole[J].Journal of Safety Science and Technology,2016,12(5):139-145.
[4] 王兆丰,武炜.煤矿瓦斯抽采钻孔主要封孔方式剖析[J].煤炭科学技术,2014,42(6):31-34,103.
WANG Zhaofeng,WU Wei.Analysis on major borehole sealing methods of mine gas drainage boreholes[J].Coal Science & Technology,2014,42(6):31-34,103.
[5] 郝志勇.材料复合技术及其在钻孔密封中的应用研究[D].徐州:中国矿业大学,2010:14-15.
HAO Zhiyong.Research of composite technology and application in bored sealiing[D].Xuzhou:China University of Mining and Technology,2010:14-15.
[6] 王振锋,周英,孙玉宁,等.新型瓦斯抽采钻孔注浆封孔方法及封堵机理[J].煤炭学报,2015,40(3):588-595.
WANG Zhenfeng,ZHOU Ying,SUN Yuning,et al.Novel gas extraction borehole grouting sealing method and sealing mechanism[J].Journal of China Coal Society,2015,40(3):588-595.
[7] 靳钟铭,赵阳升,贺军,等.含瓦斯煤层力学特性的实验研究[J].岩石力学与工程学报,1991,10(3):271-280.
JIN Zhongming,ZHAO Yangsheng,HE Jun,et al.An experimental study on the mechanical properties of gas-bearing coal seams[J].Chinese Journal of Rock Mechanics & Engineering,1991,10(3):271-280.
[8] 王云飞,龚健,陈赞成.不同围压下煤岩变形与剪胀扩容模型[J].水文地质工程地质,2015,42(1):106-111.
WANG Yunfei,GONG Jian,CHEN Zancheng.Deformation characteristics and dilatancy model of coal rock under different confining pressures[J].Hydrogeology & Engineering Geology,2015,42(1):106-111.
[9] 陈进,袁文伯.巷道围岩的脆性破坏理论[J].工程力学,1989,6(2):134-137.
CHEN Jin,YUAN Wenbo.A brittle failure theory of the rock mass around tunnel[J].Engineering Mechanics,1989,6(2):134-137.
[10] 付国彬.巷道围岩破裂范围与位移的新研究[J].煤炭学报,1995(3):304-310.
FU Guobin.Recent investigation of extent of fractured zone and displacement of rocks around the roadways[J].Journal of China Coal Society,1995(3):304-310.
[11] 范文,俞茂宏,陈立伟,等.考虑剪胀及软化的洞室围岩弹塑性分析的统一解[J].岩石力学与工程学报,2004(19):3213-3220.
FAN Wen,YU Maohong,CHEN Liwei,et al.Unified elastoplastic solution for surrounding rocks of openings with consideration of material dilatancy and softening[J].Chinese Journal of Rock Mechanics & Engineering,2004,23(19):3213-3220.
[12] 姚国圣,李镜培,谷拴成.考虑岩体扩容和塑性软化的软岩巷道变形解析[J].岩土力学,2009,30(2):463-467.
YAO Guosheng,LI Jingpei,GU Shuancheng.Analytic solution to deformation of soft rock tunnel considering dilatancy and plastic softening of rock mass[J].Rock & Soil Mechanics,2009,30(2):463-467.
[13] 潘阳,赵光明,孟祥瑞.非均匀应力场下巷道围岩弹塑性分析[J].煤炭学报,2011,36(S1):53-57.
PAN Yang,ZHAO Guangming,MENG Xiangrui.Elasto-plastic analysis on surrounding rock mass under non-uniform stress field[J].Journal of China Coal Society,,2011,36(S1):53-57.
[14] 郝富昌,孙丽娟,刘明举.考虑塑性软化和扩容特性的最短封孔深度研究[J].中国矿业大学学报,2014,43(5):789-793,807.
HAO Fuchang,SUN Lijuan,LIU Mingju.Study of shortest sealing depth with considering plastic softening and dilatancy[J].Journal of China University of Mining & Technology,2014,43(5):789-793,807.
[15] 武炜.水泥基复合材料带压注浆封孔测压技术研究[D].焦作:河南理工大学,2015:25-29.
WU Wei.Study on coal seam gas pressure measuretechnology of grouting with pressure drillingsealing base on the cement compositematerials[D].Jiaozhuo:Henan Polytechnic University,2015:25-29.
[16] 董方庭,宋宏伟,郭志宏,等.巷道围岩松动圈支护理论[J].煤炭学报,1994(1):21-32.
DONG Fangting,SONG Hongwei,GUO Zhihong,et.al.Roadway support theory based on broken rock zone[J].Journal of China Coal Society,1994(1):21-32.
[17] 袁文伯,陈进.软化岩层中巷道的塑性区与破碎区分析[J].煤炭学报,1986(3):77-86.
YUAN Wenbo,CHEN Jin.Analysis of plastic zone and loose zone around opening in softening rockmass[J].Journl of China Coal Society,1986,11(3):77-85.
[18] 李世平,吴振业,贺永年,等.岩石力学简明教程[M].北京:煤炭工业出版社,1996:90-100.
[19] 沈明荣,陈建峰.岩体力学[M].上海:同济大学出版社,2006:153-155.
[20] 何满潮,景海河,孙晓明.软岩工程力学[M].北京:科学出版社,2002:114-116.
[21] 郑颖人,朱合华,方正昌,等.地下工程围岩稳定分析与设计理论[M].北京:人民交通出版社,2012:60-68.