
移动阅读
井下目标精确定位是煤矿安全高效生产的重要保障,同时也是矿井人员定位研究的主要方向[1-2]。目前,矿井人员定位系统主要采用基于测距的定位技术[3-4]。TOA(Time of Arrive)是一种基于信号到达时间的精确测距定位技术,在矿井定位领域得到了广泛应用。文献[5-6]指出由于煤矿井下通信空间受限,对无线信号的传输形成了巨大干扰,导致TOA定位精度易受计时误差、同步时延和NLOS时延等误差因素的影响。
文献[7]提出了一种多点定位TOA精确估计及同步误差矫正算法,能够有效消除同步时延和计时误差对TOA定位精度的影响,但并未考虑矿井巷道中存在大量的固定设备设施和移动运输工具等造成的电磁波NLOS 时延误差。文献[8]提出了改进均值滤波和参数拟合的方法来抑制巷道NLOS时延误差,但优化后的TOA定位误差在0~3 m,不能满足当前煤矿的需求。文献[9]提出了卡尔曼滤波和指纹定位的方法,该方法能够有效抑制巷道NLOS时延,但对卡尔曼滤波进行改进时未考虑连续出现多次巷道随机NLOS时延的情况,且指纹采集工作量大不利于实际应用。
笔者在消除计时误差和同步时延的基础上,通过对巷道NLOS时延误差的成因和特性分析,提出了一种消除巷道NLOS时延误差的矿井TOA定位方法。
TOA定位技术是基于信号到达时间的一种测距方法,主要是通过获取电磁波信号在发射端和接收端之间的传播时间,计算发射端与接收端之间的距离来达到定位的目的,即
d=ctTOA
(1)
式中,d为移动目标与信标基站间的距离;c为电磁信号在空气中的传播速度,约为光速;tTOA为电磁波信号传播的实际时间,为发射设备和接收设备之间的同步时延。
因为c=3.0×108 m/s,微小的时间误差都会导致无法忽略的距离偏差,所以TOA技术对时间同步精度要求很高。在实际测量中,实际测量时间主要包含有计时误差、时间同步误差、NLOS时延误差,若记实际测量时间为tz,则有
tz=tTOA+ts+te+tNLOS
(2)
式中,te为发射设备和接收设备之间的同步时延;ts为由计时器频率偏移导致的计时误差;tNLOS为NLOS时延。
文献[10]提出了一种采用对称双边双路测距算法(SDS-TWR)消除ts以及te的方法。SDS-TWR方法的原理如图1所示。

图1 SDS-TWR方法原理
Fig.1 Schematic diagram of the SDS-TWR method
SDS-TWR方法包括2次双路对称测量。第1次测量基站A向基站B发送信号的时间,第2次测量基站B向基站A发送信号的时间。如图1所示,两基站间的距离d为
(3)
通过上述方法,同步时延ts和计时误差te对TOA定位精度的影响将会消除,式(2)变换为
tz=tTOA+tNLOS
(4)
因此,如何有效抑制NLOS时延是TOA精确定位的关键。
电磁波的NLOS(Non Line of Sight)传播是由于电磁波信号传播环境中存在障碍物,致使信号无法按照直射径传播,而是通过反射等方式传播迫使电磁波传输路径变长的一种现象[11-12]。因此在进行TOA测距时,TOA测量值中不可避免的包含了由电磁波NLOS传播所引起的误差,即NLOS时延误差。
文献[13]提出了NLOS时延模型。文献[9]在NLOS时延模型的基础上将NLOS时延扩展为
tNLOS=Tτdθξ
(5)
其中,Tτ为已知固定参数,等于信号发射端与接收端间相距1 km时的中值;θ为0.5~1.0的常数;d为信号发射端与接收端间距离;ξ为服从对数分布的随机变量,即10lg ξ均值为0、标准差δξ为4~6 dB的高斯随机变量。
由于矿井巷道中存在着大量的基建设施、生产设备和安全设备等固定设施,且这些固定设施以相同的单位体积或截面在同一段巷道内沿巷道走向设置,从而造成了相对稳定、具有一定规律性的巷道固定NLOS时延。巷道中还存在机车等移动设备,它们会使巷道内的电磁波传播环境发生随机的变化,从而形成了具有显著性、随机性、难以定量分析等特点的巷道随机NLOS时延。由于巷道随机NLOS时延和巷道固定NLOS时延形成的误差均具有正向性,所以应针对巷道不同NLOS时延的特点,设计相应的算法对其进行抑制,从而达到提高TOA定位精度的目的。
由前文分析可知,矿井TOA定位误差主要由同步时延、计时误差和NLOS时延组成。本文在采用SDS-TWR方法消除同步时延和计时误差的基础上,结合矿井巷道NLOS时延的特点,对于由巷道中的移动装置和非规律性设备等引起的巷道随机NLOS时延误差,采用改进卡尔曼滤波器的预估值替代测量过程中偏差较大的数据来进行抑制;而对于由巷道固定设施和规律性设备等造成的巷道固定NLOS时延误差,采用参数拟合建立巷道固定NLOS时延模型抑制其造成的TOA测距正向偏移误差。同时由于本文采用一维定位算法,将矿井巷道理想化为一条直线,而实际巷道是一个具有一定宽度的平面,从而造成滤除NLOS时延的TOA定位点漂移的现象,故采用几何算法对估计位置进行归一化处理。
在图2所示的矿井TOA定位的系统结构图中,矿井巷道以具有分支的带状和条状为主要分布形式,宽度为2.0~4.4 m,高度为1.6~3.5 m。定位检测基站按照巷道的实际走向,采用直线方式安装在巷道顶板中点,相邻两个基站间距为60 m,且均配备有双向定向天线检测信号方向。井下作业人员携带识别卡在巷道中以0~2 m/s的速度移动,机车等移动设备按照既定路线以5 m/s的速度匀速运动。系统模型和数据处理流程如下所述。
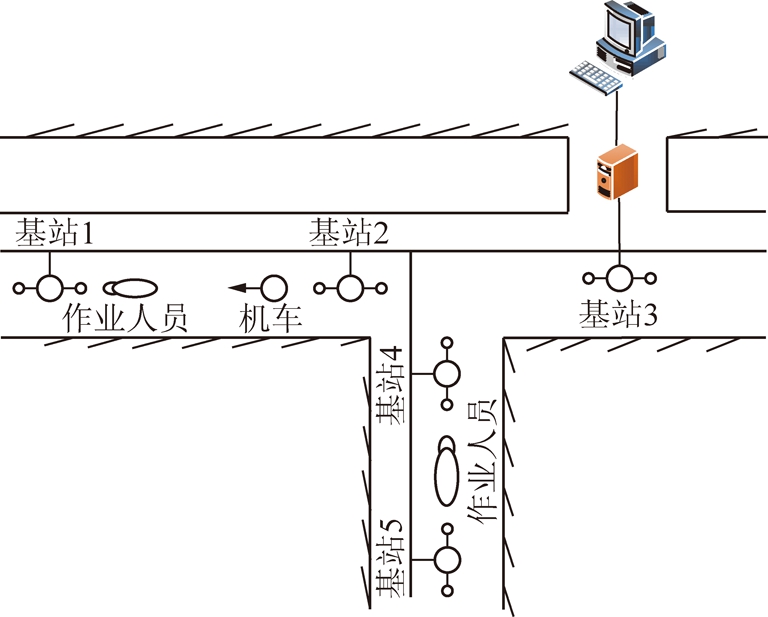
图2 矿井TOA定位的系统结构
Fig.2 System structure diagram of mine TOA positioning
(1)人员识别卡以采样时间间隔ΔT分别向最近的2个基站发送检测信号。假定2个基站的编号分别是i和i+1。
(2)基站i和基站i+1分别利用SDS-TWR方法消除tsi,ts(i+1)以及tei和te(i+1)后将tzi和tz(i+1)的值上传至地面服务器。
(3)服务器利用改进卡尔曼滤波器将接受到的tzi和tz(i+1)值中的巷道突发NLOS时延滤除,并将时间数据转化为距离数据![]() 和
和![]()
(4)服务器依据参数拟合建立的巷道固定NLOS时延方程解得井下作业人员的估计位置di和di+1,之后通过几何算法对估计位置进行归一化处理,得到井下作业人员准确位置![]() 和
和![]()
卡尔曼滤波的基础理论是采用由状态方程和观测方程组成的状态空间模型来描述动态系统[14-15],即
X(k+1)=ΦX(k)+W(k)
(6)
Y(k)=HX(k)+V(k)
(7)
式中,k为离散时间,系统在时刻k的状态为X(k)∈Rn;Y(k)∈Rm为对应状态的观测信号;W(k)∈Rn为输入的白噪声;V(k)∈Rm为观测噪声;Φ为状态转移矩阵;H为观测矩阵;n,m为矩阵的维数。
若假设W(k)和V(k)是均值为0、方差阵各为Q和R的不相关白噪声,即
E(W(k))=0
(8)
E(V(k))=0
(9)
E(W(k)WT(j))=Qδkj
(10)
E(V(k)VT(j))=Rδkj
(11)
E(W(k)VT(j))=0
(12)
其中,E为求取均值;k,j为任意数,且δkk=1,δkj=0。假设W(k)和V(k)与初始状态X(0)不相关,即
E(X(0))=μ0
(13)
E[(X(0)-μ0)(X(0)-μ0)T]=P0
(14)
卡尔曼滤波的实质是把某时刻的状态量与当前时刻的测量值联系起来,以某种最优的方式求解当前状态X(j)的线性最小方差估计值![]() 的问题
的问题![]() 的极小化性能指标为
的极小化性能指标为
(15)
卡尔曼滤波的递推过程如下:
(16)
![]()
(17)
![]()
(18)
![]()
(19)
![]()
(20)
![]()
(21)
式中,![]() 和
和![]() 分别为第k个时刻状态变量的预测值和估计值;
分别为第k个时刻状态变量的预测值和估计值;![]() 和
和![]() 分别为第k个时刻状态变量的预测误差和估计误差的协方差矩阵;ε(k)为测量矩阵Y(k)对应的新息值;In为n阶单位矩阵;K(k)为第k个时刻所对应的Kalman增益。
分别为第k个时刻状态变量的预测误差和估计误差的协方差矩阵;ε(k)为测量矩阵Y(k)对应的新息值;In为n阶单位矩阵;K(k)为第k个时刻所对应的Kalman增益。
在本文中,卡尔曼滤波器主要是用于消除巷道随机NLOS误差,所以将卡尔曼递推过程中大于阈值ΔE的新息值ε(k)用前一次新息值ε(k-1)覆盖,再进行本次的迭代运算。因此迭代过程中,式(20)变换为

(22)
ε(k)=ε(k-1) (ε(k)>ΔE)
(23)
新息阈值ΔE需要根据不同类型巷道内影响因素,如人员运动特点、机车移动速度等对实际测量的影响程度进行设定,若阈值ΔE过大,则可能造成巷道突发NLOS时延不能有效滤除;若阈值ΔE过小,则会造成仅包含有巷道固定NLOS时延误差的TOA测量值非法舍弃,影响定位精度。
本文方法新息阈值ΔE应当满足不小于作业人员在一个采样时间间隔ΔT内运动的最大距离Smax所对应的TOA值,且不大于最大测量误差ΔSmax所对应的TOA值。本文通过大量仿真研究和实验验证,得出了ΔE=(1.15~1.25)Smax/c的数学公式,c为光速。
本文卡尔曼滤波器的参数如下:
(24)
![]()
(25)
![]()
(26)
![]()
(27)
![]()
(28)
![]()
(29)
![]()
(30)
![]()
(31)
Vi(k)=REi
(32)
Vi+1(k)=RE(i+1)
(33)
式中,tTOAi(k)和tTOA(i+1)(k)分别为第i个和第i+1个基站的TOA待估计值;![]() 和
和![]() 分别为一阶导数;ΔT为采样时间间隔;ωn为过程噪声;REi为第i个读卡器的测量误差,两者均需根据具体情况确定。
分别为一阶导数;ΔT为采样时间间隔;ωn为过程噪声;REi为第i个读卡器的测量误差,两者均需根据具体情况确定。
本文采用双节点几何定位方法对目标位置进行估计,设两节点间的距离为d,由于通过卡尔曼滤波消除随机NLOS时延误差的TOA测量值中还含有巷道固定NLOS时延误差,如图3所示,数据均存在正向偏移。

图3 矿井几何定位示意
Fig.3 Schematic diagram of mine geometric positioning
由前文分析可知,在同一段巷道的两节点之间,可以认为巷道固定NLOS时延分布规律相同,结合NLOS时延扩展式(5)有
(34)
式中,![]() 和
和![]() 分别为经卡尔曼滤波后的TOA测量值;d1和d2分别为抑制巷道固定NLOS时延后的TOA估计值。若设巷道NLOS时延系数p为
分别为经卡尔曼滤波后的TOA测量值;d1和d2分别为抑制巷道固定NLOS时延后的TOA估计值。若设巷道NLOS时延系数p为
p=cTτξ
(35)
将式(35)代入式(34)可得
(36)
由于巷道NLOS时延系数p和指数θ未知,因此在巷道无机车等移动设备时,对巷道中任意m点进行测量值采样。设读卡器1与这些点的实际距离分别为d1(1),d1(2),…,d1(m),测量值分别为![]() 根据m个点的实际值和测量值建立包含未知量p和θ的m(m-1)/2个二元方程组
根据m个点的实际值和测量值建立包含未知量p和θ的m(m-1)/2个二元方程组
(37)
通过求解这些二元方程组,得p和θ的解集为
Ω={(p1,θ1),(p2,θ2),…,(pm(m-1)/2,θm(m-1)/2)}
(38)
设μp,μθ分别为p和θ的均值,即
(39)
![]()
(40)
则每组(p,θ)到解集中心点(μp,μθ)的欧氏距离为
(41)
其中,k=1,2,…,m(m-1)/2。故将最小欧氏距离min(dk)所对应的一组数值解(pk,θk)作为p和θ的参数拟合值。因此,式(36)对应的抑制巷道固定NLOS时延的计算公式为
(42)
由于通过参数拟合处理得到的TOA估计值,误差不可能被完全抑制,d1+d2=d不一定成立,故需要采用几何算法对目标位置进一步估计,即
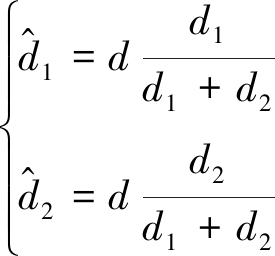
(43)
式中,![]() 和
和![]() 分别为目标的估计位置与基站A和基站B的距离。
分别为目标的估计位置与基站A和基站B的距离。
文献[9]在永城煤电集团有限责任公司的实训基地进行了测量,实验环境是具有机车轨道的平直巷道,现场示意如图2所示。两基站间的距离为60 m,基站1周围固定设备较多,携带识别卡的作业人员沿着基站1到基站2的方向,以约1.5 m/s的速度匀速前进,机车随机的在基站1与基站2之间移动,定位检测的采样时间间隔ΔT=2 s,卡尔曼滤波的新息阈值ΔE=5/c。实验数据[9]见表1。
本文以表1中的实际数据和测量数据所对应的时间值建立卡尔曼滤波的状态方程X(k)和测量方程Y(k),然后分别经卡尔曼滤波器和改进卡尔曼滤波器处理,并根据式(1)将时间数据转化为距离数据,得到不同方法的定位结果(表1),定位曲线和误差曲线分别如图4,5所示。由表1和图4,5可知,当实验在第7,11,19,20次进行定位检测时,机车正好移动到了作业人员与定位基站之间,产生了随机NLOS时延误差;测量数据经过卡尔曼滤波处理之后,巷道随机NLOS时延误差有一定程度的减小,但并未完全滤除;测量数据经过基于新息阈值的卡尔曼滤波器处理之后,巷道随机NLOS时延误差基本滤除,误差曲线趋于平稳,但是定位误差仍然保持在1.9~3.1 m。从而表明基于新息阈值的卡尔曼滤波器能够有效滤除巷道随机NLOS时延误差,但不能对巷道固定NLOS时延误差有明显的抑制作用。
在改进卡尔曼滤波器处理结果的基础上通过参数拟合求得巷道NLOS时延系数p=2.596 4和指数θ=0.096 5,结合几何算法后的定位结果(表1),定位曲线和误差曲线分别如图6,7所示。
由表1和图6,7可知,定位数据在经改进卡尔曼滤波器处理的基础上,通过参数拟合和几何算法处理后,定位误差由1.9~3.1 m下降到了0~0.8 m,平均误差由2.4 m降为0.3 m。从而表明在改进卡尔曼滤波器滤除巷道随机NLOS时延误差的基础上,参数拟合和几何算法能够有效抑制巷道固定NLOS时延误差。不同方法的定位结果见表2,误差数据见表3,误差曲线如图8所示。
表1 实验和仿真数据
Table 1 Experimental and simulation data m

测量次数实际位置(d1,d2)文献[9]的测量位置(d1,d2)卡尔曼滤波器估计位置(d1,d2)改进卡尔曼滤波器估计位置(d1,d2)本文所提方法的估计位置(d1,d2)1(0,60)(3.7,63.7)(0,60.0)(0,60.0)(0,60.0)2(3,57)(12.3,59.5)(11.7,59.3)(4.9,58.9)(2.2,57.8)3(6,54)(9.5,57.2)(10.9,57.2)(9.3,57.1)(6.3,53.7)4(9,51)(17.1,53.8)(15.8,54.1)(14.3,54.1)(9.8,50.2)5(12,48)(14.2,50.6)(15.8,50.9)(15.8,50.9)(12.6,47.4)6(15,45)(16.8,47.3)(17.1,47.6)(17.8,47.7)(14.8,47.2)7(18,42)(19.7,49.3)(19.3,47.0)(20.2,44.3)(17.6,42.4)8(21,39)(28.5,41.1)(24.4,43.0)(22.5,41.2)(20.2,39.8)9(24,36)(26.9,38.5)(26.9,39.5)(25.9,38.3)(23.6,36.4)10(27,33)(33.6,35.1)(31.0,36.1)(29.3,35.1)(27.0,33.0)11(30,30)(32.2,38.1)(33.3,34.8)(32.2,32.1)(30.0,30.0)12(33,27)(37.2,9.5)(36.4,31.3)(35.1,29.2)(33.1,29.9)13(36,24)(39.3,26.3)(39.2,27.8)(38.4,26.2)(36.3,23.7)14(39,21)(41.4,21.9)(41.8,24.6)(41.4,23.4)(39.3,20.7)15(42,18)(48.2,21.2)(45.5,21.6)(44.4,20.6)(42.2,17.8)16(45,15)(46.9,17.8)(48.0,18.4)(47.2,17.7)(45.2,14.8)17(48,12)(50.1,15.0)(50.7,15.3)(50.2,14.8)(48.1,11.9)18(51,9)(53.6,11.6)(53.5,12.2)(53.2,11.7)(51.2,8.8)19(54,6)(57.8,13.9)(56.6,10.1)(56.5,8.7)(54.2,5.8)20(57,3)(63.1,10.9)(60.2,7.9)(59.8,5.7)(57.1,2.9)21(60,0)(65.9,2.8)(63.6,4.7)(63.1,2.8)(59.6,0.4)

图4 改进卡尔曼滤波器处理后的定位曲线
Fig.4 Positioning curves after being processed by improved Kalman filter

图6 消除NLOS时延后的定位曲线
Fig.6 Positioning curves after eliminating NLOS delay

图5 改进卡尔曼滤波器处理后的误差曲线
Fig.5 Error curves after after being processed by improved Kalman filter

图7 消除NLOS时延后的误差曲线
Fig.7 Error curves after eliminating NLOS delay
表2 不同方法定位结果
Table 2 Positioning results of different methods m

测量次数实际位置(d1,d2)/mSDS-TWR方法估计位置(d1,d2)卡尔曼滤波和指纹定位估计位置[9](d1,d2)卡尔曼滤波和参数拟合估计位置(d1,d2)改进卡尔曼滤波和参数拟合估计位置(d1,d2)1(0,60)(3.7,63.7)(1,59)(0,60.0)(0,60.0)2(3,57)(12.3,59.5)(5,55)(8.0,52.0)(2.2,57.8)3(6,54)(9.5,57.2)(7,53)(7.6,52.4)(6.3,53.7)4(9,51)(17.1,53.8)(10.50)(9.8,50.2)(9.8,50.2)5(12,48)(14.2,50.6)(13,47)(12.6,47.4)(12.6,47.4)6(15,45)(16.8,47.3)(15,45)(14.4,45.6)(14.8,47.2)7(18,42)(19.7,49.3)(18,42)(16.1,43.9)(17.6,42.4)8(21,39)(28.5,41.1)(22,37)(20.9,39.1)(20.2,39.8)9(24,36)(26.9,38.5)(24,36)(23.7,36.3)(23.6,36.4)10(27,33)(33.6,35.1)(26,34)(27.5,32.5)(27.0,33.0)11(30,30)(32.2,38.1)(29,32)(29.3,30.7)(30.0,30.0)12(33,27)(37.2,9.5)(32,28)(32.5,27.5)(33.1,29.9)13(36,24)(39.3,26.3)(35,25)(35.6,24.4)(36.3,23.7)14(39,21)(41.4,21.9)(39,21)(38.6,21.4)(39.3,20.7)15(42,18)(48.2,21.2)(42,18)(41.8,18.2)(42.2,17.8)16(45,15)(46.9,17.8)(46,14)(44.8,15.2)(45.2,14.8)17(48,12)(50.1,15.0)(49,11)(47.8,12.2)(48.1,11.9)18(51,9)(53.6,11.6)(51,9)(50.8,9.2)(51.2,8.8)19(54,6)(57.8,13.9)(54,6)(53.0,7.0)(54.2,5.8)20(57,3)(63.1,10.9)(56,3)(55.2,4.8)(57.1,2.9)21(60,0)(65.9,2.8)(60,0)(58.2,1.8)(59.6,0.4)
表3 不同方法误差数据
Table 3 Error data of different methods m

测量次数SDS-TWR方法误差方法误差卡尔曼滤波和指纹定位卡尔曼滤波和参数拟合改进卡尔曼滤波和参数拟合13.71.00025.92.05.00.833.41.01.60.345.51.00.80.852.41.00.60.662.100.60.274.501.90.484.81.50.10.892.700.30.4104.41.00.50115.21.50.70.1123.41.00.50.1132.81.00.40.3142.700.40.3154.700.20.2162.410.20.2172.610.20.2182.600.20.2195.901.00.2207.00.51.80.1214.401.80.4AVG3.90.70.90.3

图8 不同方法的误差比较曲线
Fig.8 Error comparison curves on different methods
由表2,3和图8可知,用SDS-TWR方法测取的含有巷道NLOS时延误差的原始数据,误差在2.1~7.0 m,平均误差为3.9 m;采用卡尔曼滤波和指纹定位方法滤除巷道NLOS时延误差后,定位误差在0~2.0 m,平均误差为0.7 m;采用卡尔曼滤波和参数拟合方法滤除巷道NLOS时延误差后,定位误差在0~5 m,平均误差为0.9 m;采用本文提出的改进卡尔曼滤波和参数拟合方法滤除巷道NLOS时延误差后,定位误差在0~0.8 m,平均误差为0.3 m,且该方法的平均定位误差较前面3种方法分别减小了3.4,0.4和0.6 m。从而表明,笔者所提方法能够有效抑制TOA定位误差,较其他定位方法定位误差明显减小。
本文以基站2的数据为例,对本文所提方法中卡尔曼滤波新息阈值ΔE和参数拟合值p,θ取不同值时的定位误差进行仿真实验分析,数据结果见表4,5,误差曲线如图9,10所示。

图9 不同新息阈值的误差曲线
Fig.9 Error curves on different innovation thresholds

图10 不同参数拟合值的误差曲线
Fig.10 Error curves of different parameter fitting values
由表4、图9可知,当ΔE取小于其左侧边界值的0.1/c时,由于ΔE取值过小,造成改进卡尔曼滤波器在滤除随机NLOS时延的同时,将仅包含有巷道固定NLOS时延的TOA测量值非法舍弃,导致处理后的误差曲线无法趋于平稳,定位误差呈上升趋势;当ΔE取正常值5/c时,巷道随机NLOS时延误差基本滤除,误差曲线趋于平稳,定位误差保持在1.9~3.1 m;当ΔE取大于其右侧边界值的10/c时,由于ΔE取值过大,巷道随机NLOS时延误差有一定程度的减小,但并未完全滤除,误差曲线仍存在大幅波动。
由表5和图10可知,在ΔE取正常值5/c的基础上,(p,θ)分别取均值(2.753 2,0.140 4)、最小欧式距离解(2.596 4,0.096 5)和最大欧氏距离解(1.401 4,087 05)时,平均定位误差分别为0.44,0.30和0.72 m,且最小欧氏距离解的误差曲线明显优于其他两者的误差曲线。
表4 不同新息阈值的误差数据
Table 4 Error data of different innovation thresholds

测量次数测量误差/mΔE=0.1/cΔE=5/cΔE=10/c13.7000022.500.091.872.3333.200.203.053.1642.800.363.113.0852.600.552.942.8762.300.772.672.5977.300.992.294.9882.101.222.184.0192.501.452.273.55102.101.692.193.08118.101.942.104.80122.502.182.194.27132.302.372.203.82142.902.562.373.63153.202.752.583.56162.802.922.653.41173.003.102.753.33182.603.152.753.19197.903.202.744.14207.903.242.734.94212.803.292.764.65AVG3.671.812.403.50
表5 不同参数拟合值的误差数据
Table 5 Error data of different parameter fitting values

测量次数测量误差/mΔE=5/cp=2.753 2θ=0.140 4p=2.596 4θ=0.096 5p=1.401 4θ=0.870 513.7000022.501.000.820.8833.200.030.261.5342.801.510.792.6652.600.290.571.3662.300.400.150.5277.300.650.430.1182.100.950.770.3592.500.550.430.17102.100.070.020.10118.100.080.080.08122.500.150.090.03132.300.420.310.05142.900.440.270.11153.200.400.180.34162.800.410.160.53173.000.390.110.76182.600.450.150.94197.900.460.171.17207.900.310.091.50212.800.380.392.02AVG3.670.440.300.72
综上所述,在合理选取新息阈值ΔE和参数拟合值p和θ的基础上,本文所提方法对TOA定位误差具有较明显的抑制作用,能够实现TOA方法在井下人员定位中的有效应用。
(1)提出基于新息阈值的卡尔曼滤波算法,消除了巷道随机NLOS时延造成的脉冲噪声对TOA测量值的影响,有效抑制了TOA定位中由巷道中机车等移动设备以及不规律设置设备引起的定位误差。
(2)在新息阈值的卡尔曼滤波算法的基础上,提出了参数拟合和几何定位算法。该算法通过参数拟合和几何定位算法的巧妙结合,有效消除了井下固有设备引起的巷道固定NLOS时延对TOA测量值的影响,成功抑制了TOA定位点的漂移现象,实现了井下目标位置的精确估计。
(3)仿真实验发现,本文所提方法平均定位误差为0.3 m,相比于SDS-TWR方法、卡尔曼滤波和指纹定位方法以及卡尔曼滤波和参数拟合方法,平均定位误差分别降低了3.4,0.4和0.6 m。从而表明本文所提方法能够有效抑制TOA定位误差,可以实现TOA方法在矿井NLOS环境中的有效应用。
[1] 胡青松,张申,吴立新,等.矿井动目标定位:挑战、现状与趋势[J].煤炭学报,2016,41(5):1059-1068.
HU Qingsong,ZHANG Shen,WU Lixin,et al.Localization techniques of mobile objects in coal mines:Challenges,solutions and trends[J].Journal of China Coal Society,2016,41(5):1059-1068.
[2] 霍振龙.矿井定位技术现状和发展趋势[J].工矿自动化,2018,44(2):51-55.
HUO Zhenlong.Status and development trend of mine positioning technology[J].Industry and Mine Automation,2018,44(2):51-55.
[3] SHAO Xiaoqiang,LI Kangle,CHEN Xi.A method of TOA positioning for mine to effectively reduce the impact of Non-Line of sight error propagation[A].Proceedings of the 30th Chinese Control and Decision Conference,CCDC 2018[C].Shenyang:Institute of Electrical and Electronics Engineers Inc.,2018:4650-4655.
[4] KALPANA R,BASKARAN M.TAR:TOA-AOA based random tran-smission directed localization[J].Wireless Personal Communications,2016,90(2):1-14.
[5] WANG Peng,HE Jie,XU Liyuan,et al.Characteristic modeling of TOA ranging error in rotating anchor-based relative positioning[J].IEEE Sensors Journal,2017,17(23):7945-7953.
[6] 赵泰洋,郭成安.基于接收信号强度的非视距检测与修正算法[J].数据采集与处理,2014,29(3):397-402.
ZHAO Taiyang,GUO Cheng’an.NLOS detection and mitigation algorithm using received signal strength[J].Journal of Data Acquisition and Processing,2014,29(3):397-402.
[7] 王洪,金尔文,刘昌忠,等.多点定位TOA精确估计及同步误差校正算法[J].系统工程与电子技术,2013,35(4):835-839.
WANG Hong,JIN Erwen,LIU Changzhong,et al.Accurate estimation of TOA and calibration of synchronization error for multilateration[J].Systems Engineering and Electronic,2013,35(4):835-839.
[8] 孙继平,李晨鑫.基于改进均值滤波和参数拟合的矿井TOA几何定位方法[J].煤炭学报,2015,40(5):1206-1212.
SUN Jiping,LI Chenxin.Mine TOA geometric positioning method based on improved mean filtering and parameter fitting[J].Journal of China Coal Society,2015,40(5):1206-1212.
[9] 孙继平,李晨鑫.基于卡尔曼滤波和指纹定位的矿井TOA定位方法[J].中国矿业大学学报,2014,43(6):1127-1133.
SUN Jiping,LI Chenxin.Mine time of arrival positioning method based on Kalman filtering and fingerprint positioning[J].Journal of China University of Mining & Technology,2014,43(6):1127-1133.
[10] 王明东,戴亚文,范俊,等.基于UWB技术的隧道无线定位方法研究[J].武汉理工大学学报,2016,38(8):56-60.
WANG Mingdong,DAI Yawen,FAN Jun,et al.Research of wireless tunnel positioning method based on UWB Technology[J].Journal of Wuhan University of Technology,2016,38(8):56-60.
[11] CHENG Long,WANG Yan,SUN Xingming,et al.A mobile localization strategy for wireless sensor network in NLOS conditions[J].China Communications,2016,13(10):69-78.
[12] 黄越洋,张嗣瀛,井元伟,等.基于TDOA和RSS的可行域粒子滤波非视距定位算法[J].控制与决策,2017,32(8):1415-1420.
HUANG Yueyang,ZHANG Siying,JING Yuanwei,et al.Non-line of sight localization algorithm based on TDOA and RSS by feasible region particle filter[J].Control and Decision,2017,32(8):1415-1420.
[13] 赵军辉,张雪雪,曾龙基.提高NLOS环境下室内定位精度的新方法[J].北京邮电大学学报,2012,35(6):38-43.
ZHAO Junhui,ZHANG Xuexue,ZENG Longji.An approach to improving the accuracy of the indoor positioning with NLOS Environment[J].Journal of Beijing University of Posts and Telecommunications,2012,35(6):38-43.
[14] ZHOU Cheng,YUAN Jiazheng,LIU Hongzhe,et al.Bluetooth indoor positioning based on rssi and kalman filter[J].Wireless Personal Communications,2017,96(3):4115-4130.
[15] 周瑞,袁兴中,黄一鸣.基于卡尔曼滤波的WiFi-PDR融合室内定位[J].电子科技大学学报,2016,45(3):399-404.
ZHOU Rui,YUAN Xingzhong,HUANG Yiming.WiFi-PDR fused indoor positioning based on Kalman filtering[J].Journal of University of Electronic Science and Technology of China,2016,45(3):399-404.