随着煤炭资源开采向深部发展,资源地质赋存条件更加的复杂,煤岩与瓦斯的赋存环境处于高地应力、高地温、高渗透压[1]的状态,导致煤与瓦斯突出矿井和突出煤层数量不断增加,瓦斯突出灾害的发生次数和突出强度相比于浅部煤层呈现上升趋势。瓦斯同时又是一种高效的清洁能源[2],若能得到合理开发利用,可以有效地改善能源结构。研究深部煤层瓦斯抽采运移特征对煤气资源的安全高效开采具有重要意义[3-4]。
前人基于不同假设条件,针对煤岩体的孔隙率、渗透率模型进行了深入研究。SEIDLE等[5]提出了一个动态的孔隙率演化模型,该模型考虑了煤体的膨胀收缩效应。PALMER等[6]考虑了孔隙压力和基质膨胀收缩对割理裂隙的孔隙率演化影响,提出了一个基于单轴应变和恒定垂向应力假设的渗透率模型。SHI等[7]提出的渗透率模型考虑了吸附解吸引起的煤体变形,并提出了考虑水平有效应力的渗透率模型。CUI等[8]使用线弹性多孔弹性介质理论,考虑吸附解吸效应推导出了与平均有效应力有关的渗透率模型。渗透率随着有效应力的变化归根结底是孔隙率随着有效应力的变化[9]。
上述研究均未考虑时间效应对煤岩体渗透性的影响,而时间效应对于煤岩体的强度和变形有较大影响,同时也会造成渗透率的改变。在煤岩体时效特性的研究方面,周辉等[10]通过分析岩石破裂过程中强度的演化规律和机制,建立了岩石强度时效性演化模型,定量描述了恒定应力条件下岩石强度的弱化过程,从理论和机制上解释了岩石强度的时间效应问题。周宏伟等[11] 从分数阶导数出发,在常黏性系数Abel黏壶基础上提出了一种新的变黏性系数的Abel黏壶元件。利用两种分数阶Abel黏壶代替经典西原模型中Newton黏壶的方法,建立了基于分数阶导数的盐岩流变本构模型,并给出了该模型的解析解,较好地反映了盐岩流变的三阶段尤其是加速流变阶段。尹光志等[12]对煤层顶底板岩层试件进行卸围压蠕变及周期加载蠕变实验,并采用Burgers 体模型对采动影响下的岩体进行蠕变理论分析,建立了采动下煤岩蠕变损伤模型,较好地反映岩体蠕变曲线特征。周长冰等[13]分析了高温三轴应力下气煤蠕变特征,通过对不同温度下气煤的渗透率和孔隙率的分析,可以初步判断气煤蠕变特征发生变化的临界温度。许江等[14]进行了考虑时间效应的蠕变对含瓦斯煤渗透率影响的试验分析,发现在相同温度和有效应力条件下,经历蠕变后煤的渗透率会降低。郝富昌等[15]建立了钻孔周围煤体黏弹塑性模型和蠕变-渗流耦合作用下瓦斯运移模型,认为不同埋深钻孔均会随时间产生缩孔现象,进而确定了不同埋藏深度钻孔的有效抽采半径。
为了考虑煤岩体的时效性特征对瓦斯在煤层中运移的影响以及准确描述煤岩的孔隙率和渗透率演化过程,笔者以煤层割理裂隙的渗透性受三向应力影响的角度出发,借鉴CUI等[8]引入平均有效应力变化量来描述煤层渗透情况的思想,利用CUI等[8]建立的孔隙率、渗透率与平均有效应力变化量之间的指数关系,并结合蠕变本构建立了考虑时效性的孔隙率和渗透率模型,对比和分析了在模拟深部瓦斯运移过程中的作用。
1 考虑时效性的煤体本构方程
随着埋深的增加和瓦斯抽采时间的延长,含瓦斯煤的时效性特征越来越明显。 NISHIHARA[16]提出了准静态流变模型——西原模型,用来描述时间效应影响下岩石的应力应变关系,如图1所示。该模型中包括胡克体,黏弹性体和黏塑性体。
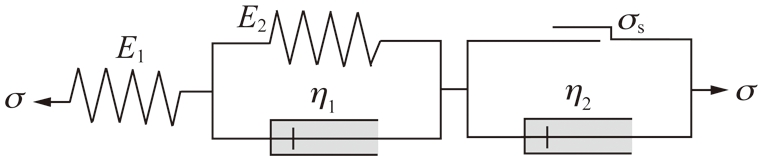
图1 经典西原模型
Fig.1 Classical Nishihara model
根据不同元件的串联方式,整个模型的总应变可表示为
ε=εe+εve+εvp
(1)
式中,εe,εve和εvp分别为胡克体、黏弹性体和黏塑性体的应变。
本文只考虑煤层所受应力小于其屈服应力σs的情况,则西原模型的蠕变本构关系可表示为
(2)
式中,Ee为煤体的弹性模量,GPa;Eve为煤体的黏弹性模量,GPa;ηve为煤体的黏塑性模量,GPa。
不考虑时间效应的应力应变本构方程由JAEGER[17]提出:
(3)
则考虑煤体基质蠕变效应、瓦斯吸附解吸的有效应力应变本构关系可由式(3)改写成
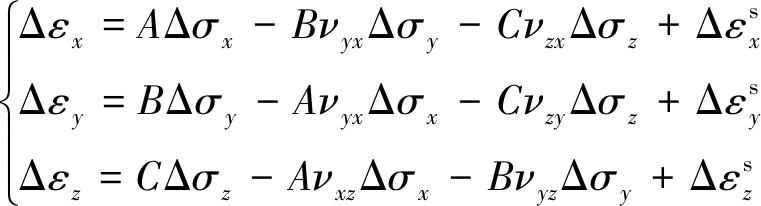
(4)
式(4)中系数A,B,C表达式为

(5)
其中,Eex,Eey,Eez分别为煤体在x,y,z方向上的弹性模量,GPa;Evex,Evey,Evez为煤体x,y,z方向上的黏弹性模量,GPa;νxy为xy平面内的泊松比;νzx和νzy为zx和zy平面内的泊松比。式(4)中煤体由吸附解吸产生的体应变![]() 已经得到了实验验证,并应用于大量的渗透率演化模型。对于Langmuir类型的吸附解吸过程,吸附体应变的表达式为
已经得到了实验验证,并应用于大量的渗透率演化模型。对于Langmuir类型的吸附解吸过程,吸附体应变的表达式为
(6)
式中,εL为Langmuir体应变常数;PL为Langmuir压力常数,MPa; p为孔隙压力,MPa。
对于煤储层,可认为其受三向应力状态,受力示意如图2所示。同时假设在钻孔周围很大范围内的煤层边界在x,y方向应变较小,可忽略不计,在z方向存在应变[15]。
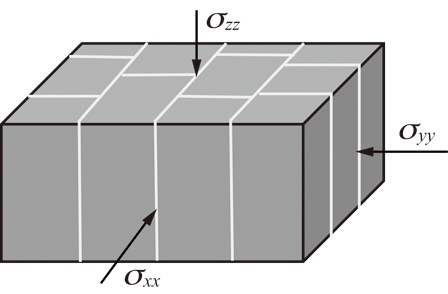
图2 煤层受力示意
Fig.2 Distribution of coal seam stress
在上述应变假设下,有效应力应变本构关系可由式(4)简化为
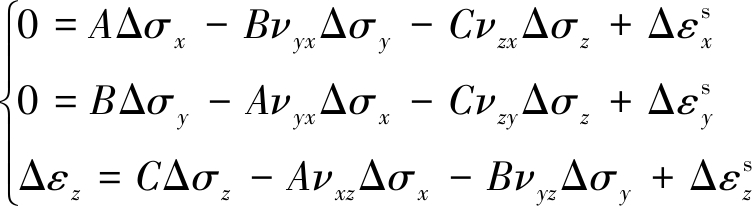
(7)
考虑上覆岩层总载荷τ不变,即Δτ =0,利用有效应力原理导出z方向的有效应力变化量,具体形式为
Δσz=Δ(τ-αp)=Δτ-Δαp=-Δαp
(8)
式中,α为Biot系数。
煤是一种典型的沉积岩,具有横观各向异性的特征,可以认为煤层在x,y方向的物理力学性质相同,而垂直于xy平面的z方向物理力学性质不同,则在x,y方向有效应力的变化量可通过式(7)变换成
![]()
(9)
则考虑时间效应的平均有效应力改变量可由式(8)和式(9)表示为
![]()
(10)
式(10)中第1项、第2项表示弹性和黏弹性割理裂隙压缩性,而第3项代表弹性和黏弹性基质收缩。其中
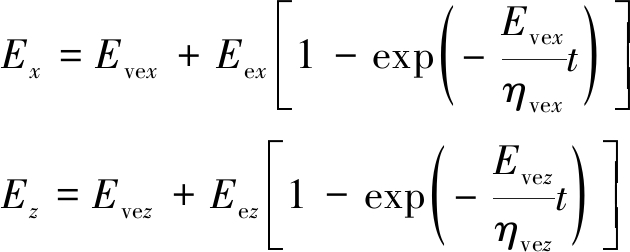
(11)
2 考虑时效性的煤体孔隙率和渗透率模型
为了计算时间效应和瓦斯吸附解吸对煤体渗透率演化的影响。笔者借助CUI-BUSTIN模型(C-B模型)的思想[8,18],在描述孔隙率与渗透率动态变化过程中引入平均有效应力变化量。CUI等[18]指出孔隙率与平均有效应力关系表示为
(12)
式中,φ0为初始孔隙率;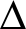 σe为平均有效应力改变量,MPa;Kp为孔隙体积模量,GPa。
σe为平均有效应力改变量,MPa;Kp为孔隙体积模量,GPa。
此外,针对孔隙体积模量Kp与煤体基质的弹性模量K之间关系可表示为
(13)
其中,E为煤体的弹性模量,GPa;ν为泊松比。将式(13)代入式(12),则孔隙率演化模型可表示为
(14)
此外,渗透率与孔隙率之间可认为满足如下幂函数关系式:
(15)
则渗透率演化可表示为
(16)
其中,cf=1/Kp 为割理裂隙压缩系数。根据所述孔隙率、渗透率与平均有效应力变化量之间的关系,将式(10)和(11)代入到式(14)和(16),导出基于时间效应考虑的孔隙率与渗透率模型:

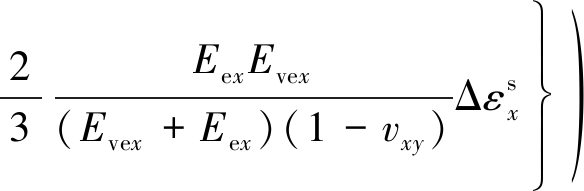
(17)

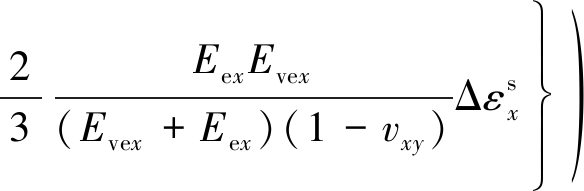
(18)
3 瓦斯运移方程
鉴于瓦斯在煤体中的流动过程较为复杂,控制方程基于如下假设构建:① 主要考虑割理裂隙渗透作用;② 瓦斯在裂隙割理中的运动规律满足达西定律,忽略气体的Klinkenberg效应;③ 利用Langmuir等温吸附方程描述气体解吸过程。
气体在流动过程中的连续性方程可表示为
 (ρv)=Qs
(ρv)=Qs
(19)
式中,H为自由项和解吸项的气体含量,kg/m3;v为气体的达西速度,m/s;ρ为气体密度,kg/m3;Qs为气体源汇项,kg/(m3·s)。
根据CUI和BUSTIN[8]在文献中表述,H可表示为
(20)
其中,ρa为标准大气压下的气体密度,kg/m3;ρc为煤的密度,kg/m3;VL是Langmuir体积常数,m3/kg;PL是Langmuir压力常数,MPa;p为气体压力,MPa。其中,气体密度可认为符合理想气体状态方程,形式为
(21)
式中,M为瓦斯气体的摩尔质量,g/mol;R为理想气体常数,J/(mol·K);T为温度,K。
一般气体渗流过程忽略重力的影响,因此,在不考虑重力影响的条件下,根据达西定律,气体流速为
 p
p
(22)
式中,μ为瓦斯气体动力黏度系数,Pa·s。
根据式(19)~(22),新的气体连续性方程可表示为

![]()
(23)
将考虑时间效应的渗透率和孔隙率演化模型代入式(23),通过COMSOL Multiphysics软件进行数值求解,从而得到同时考虑时间效应和解吸效应的瓦斯运移规律。
4 瓦斯运移特性模拟分析
4.1 计算模型及参数
计算模型如图3所示,二维均匀介质长宽均为10 m,钻孔半径为0.15 m,模型中初始瓦斯气压为6 MPa,在xy平面内,假设初始孔隙率为0.005、初始渗透率为1×10-15 m2,并且在各个方向均相等。钻孔边界处压力为0.1 MPa,煤层内与钻孔外存在气体压力差,导致气体的释放及瓦斯解吸。根据文献[19]的假设,煤体在水平面内(x,y方向)不存在应变,且在z方向上整体荷载恒定。由于模型尺寸较大,边界不受抽采影响,因此,所有边界均为不可渗边界,钻孔边界除外。模型中具有深部特征的参数来自文献[19-21],见表1。
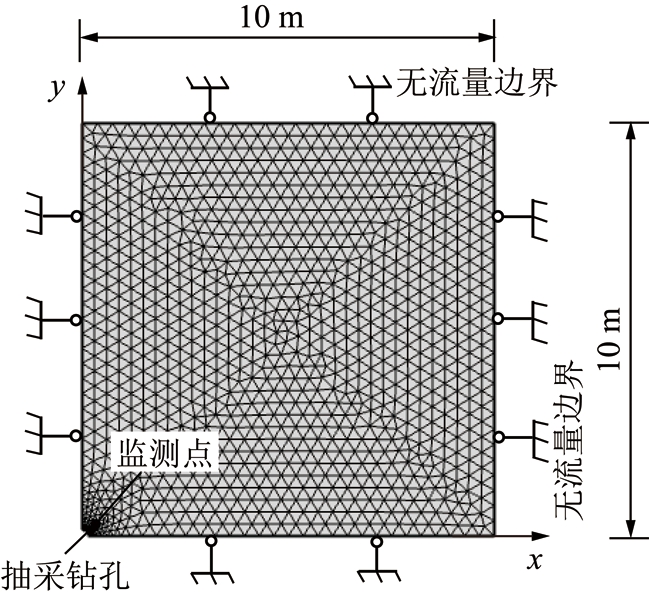
图3 数值模拟模型
Fig.3 Numerical simulation model
表1 数值模拟参数
Table 1 Numerical simulation parameters

参数数值初始孔隙率0.005煤体x,y方向弹性模量/GPa4煤体z方向弹性模量/GPa5.5xy平面内泊松比0.35zx,zy平面内泊松比0.3瓦斯动力黏度系数/(Pa·s)12.2×10-6Langmuir压力常数/MPa4.3Langmuir体积常数/(m3·kg-1)0.03Langmuir体应变常数0.012 66Biot系数1初始渗透率/10-15m21初始气体压力/MPa6割理裂隙压缩系数/MPa-10.045标准大气压瓦斯密度/(kg·m-3)0.657煤体密度/(kg·m-3)1 250煤体x,y方向黏弹性模量/GPa25煤体z方向黏弹性模量/GPa18
在模拟瓦斯长时间抽采过程中,式(11)中的![]() 一项可近似为1。因此在时间t趋于无穷大时,式(11)可简化为
一项可近似为1。因此在时间t趋于无穷大时,式(11)可简化为
(24)
通过式(24)的简化形式,认为长时间抽采过程中x,z方向的弹性系数可表示为黏弹性模量和弹性模量的线性叠加,并将式(24)代入式(17),(18)进行计算。
4.2 渗透率模型有效性验证
选取图3中距钻孔中心0.3 m的位置为监测点。为了验证本文提出的考虑时间效应模型的有效性,将本文模型、DANESH-CHEN模型[19](简称D-C模型)、现场实测数据[21]3者渗透率比率(k/k0)随瓦斯压力变化的曲线进行对比,结果如图4所示。

图4 渗透率比与压力关系
Fig.4 Relationship between permeability ratio and gas pressure
由图4可知,抽采初期瓦斯压力从6 MPa开始下降,本文考虑时间效应模型、D-C模型与现场数据拟合较好,说明在该压力区间本文模型有较好的适用性;抽采中后期即瓦斯压力小于4 MPa阶段,随着瓦斯压力逐渐下降,本文模型、D-C模型分别与现场数据存在不同程度的误差,其中D-C模型与现场数据的差别逐渐增大,而本文模型却与现场数据逐渐接近,尤其在压力为1 MPa时已经近似等于现场数据的渗透率比率。针对模拟长期瓦斯抽采,通过不同瓦斯压力阶段的对比,本文提出考虑时效性的模型优于D-C模型,能较好地模拟孔隙率、渗透率在抽采过程中动态变化情况。
本文模型在长期抽采的有效性已经验证,现讨论短期瞬态过程有效性。考虑时间效应的孔隙率、渗透率模型与其他瞬态模型存在的区别在于时间项t,现将时间t=0代入式(10),从而使式(17)和式(18)退化成未考虑时间效应的孔隙率与渗透率的演化模型,可表示为
![]()
(25)
![]()
(26)
则瞬态有效性可采用未考虑时间效应的渗透率模型式(26)验证,并与未考虑时间效应的SHI-DURUCAN模型[7](简称S-D模型)进行对比,具体趋势如图5所示。

图5 渗透率与压力关系
Fig.5 Relationship between permeability and gas pressure
图5呈现了两种未考虑时间效应的渗透率模型变化情况,随着瓦斯压力逐渐降低,渗透率呈现明显的上升趋势。抽采初期,两种模型渗透率数值差别较小,抽采中后期,两种模型渗透率数值差别明显增大。通过与图4中数据对比,发现两种未考虑时间效应模型的渗透率在数值上大于考虑时间效应下的渗透率,对比结果与许江等[14]室内蠕变渗流实验结果相同,未经历蠕变的渗透率较大。同时,图4,5呈现的曲线表明,吸附解吸作用对上述的每个渗透率模型有重要的影响,在初始储层压力6 MPa至钻孔壁标准大气压整个压力降范围内,使得渗透率随着压力降低呈指数型增长。通过对比考虑时效性模型、D-C模型在模拟瓦斯抽采时分别与现场数据的拟合程度,验证了本文提出的模型在模拟短期、长期瓦斯抽采的有效性。

图6 孔隙率、渗透率和压力随时间变化趋势
Fig.6 Evolution of porosity,permeability and pressure with time
4.3 考虑时效影响的瓦斯运移参数变化分析
图6(a)为监测点孔隙率计算结果,孔隙率随着抽采时间增长呈现增长趋势。考虑时间效应与未考虑时间效应影响模型的孔隙率变化会受到解吸效应的影响,气体解吸导致基质收缩和裂隙内瓦斯压力增大,裂隙宽度变大,孔隙率随之增大。而考虑时间效应的孔隙率明显小于未考虑时间效应模型的孔隙率,说明随着时间增长,一方面是蠕变本构中黏弹性元件的存在使得煤体更为致密,孔隙率变小,另一方面是抽采中应力重分布导致煤层2次压实,孔隙率变小。而图6(b)中渗透率变化趋势取决于孔隙率的变化,则通过图6(a)可知,渗透率会随着抽采时间增长呈现上升趋势。随着抽采时间增长,时间效应越发明显,考虑时间效应模型与未考虑时间效应模型的渗透率差值逐渐增大。
瓦斯抽采过程中压力随时间的变化情况如图6(c)所示,瓦斯压力随时间增长呈下降趋势,瓦斯储层初始压力为6 MPa,随着抽采进行,瓦斯压力下降趋势明显,且在考虑时间效应的瓦斯压力下降幅度略低于未考虑时效性模型,在90 000 s时下降到0.735 MPa。由于瓦斯解吸效应的存在,瓦斯压力受解吸气体含量和游离态气体含量控制,而瓦斯解吸量与游离态瓦斯气体压力密切相关。因此,时间效应对钻孔周围的瓦斯气体压力分布影响较小。
考虑时效性的渗透率随瓦斯压力变化的趋势如图7所示,通过对比发现在满足煤体所受应力小于其屈服强度和瓦斯压力降相同时,考虑时间效应模型和未考虑时间效应模型中渗透率随瓦斯压力变化差别明显,在同样气体压力下,前者小于后者的渗透率。究其原因,蠕变本构条件下黏弹性元件的存在,使煤体更致密,且气体解吸效应影响被弱化,随着气体压力的减小,时间效应会更为明显。

图7 渗透率与压力关系
Fig.7 Relationship between permeability and gas pressure
4.4 考虑时效影响的瓦斯运移特征分析
考虑模拟抽采钻孔周围的瓦斯运移情况,为实际瓦斯抽采过程中预估钻孔周围的渗透率与压力的变化情况提供数值参考。
由图8,9变化趋势可知,在同一抽采时刻,随着距钻孔中心距离的增大,渗透率呈现降低的趋势,瓦斯压力与渗透率的变化趋势相反,距中心距离越大,压力越高;而当临近钻孔中心时,渗透率上升幅度和瓦斯压力下降的幅度都比较大,这是由于越接近钻孔中心,煤层的卸压越明显,煤层渗透率也相应变大,瓦斯压力下降也就越明显。

图8 不同时刻渗透率演化
Fig.8 Evolution of permeability at different times

图9 不同时刻瓦斯压力演化
Fig.9 Evolution of gas pressure at different times

图10 不同时刻瓦斯压力和渗透率随演化趋势
Fig.10 Evolution of gas pressure and permeability at different times
在考虑时间效应的情况下,随着抽放时间的推移,煤层中的渗透率上升程度和瓦斯压力下降程度逐渐减小。这类趋势表明:在钻孔抽采瓦斯的初始阶段,受时间效应影响较小,瓦斯抽放量较大;而一段时间后受瓦斯压力降低和时间效应的影响瓦斯抽放量将趋于稳定。当模拟瓦斯抽采时间为1,10,30 d时,渗透率随着抽采时间的增长逐渐增大,各时刻模型内最小渗透率分别为0.4×10-14,1.6×10-14,1.81×10-14 m2;而瓦斯压力逐渐减小,各时刻模型内最大瓦斯压力分别为1.95,0.21,0.107 MPa。
不同时刻渗透率和瓦斯压力的演化趋势如图10所示。当模拟抽采时间逐渐增长时,相同位置处的渗透率逐渐增大,瓦斯压力逐渐减小,原因是受煤层内瓦斯压力降低和时间效应的影响。抽采1 d时,距钻孔中心距离最远处渗透率与瓦斯压力数值分别为3.67×10-15m2,1.95 MPa,临近钻孔中心处渗透率与瓦斯压力数值分别为13 ×10-15m2,0.387 MPa。而抽采30 d时,距钻孔中心距离最远处渗透率与瓦斯压力数值分别为18.1 ×10-15m2,0.107 MPa,临近钻孔中心处渗透率与瓦斯压力数值分别为18.2×10-15 m2,0.1 MPa,整个模型近似达到一种内外压力平衡状态。计算结果与实际深部煤层瓦斯从渗流通道运移至钻孔的过程中参数的变化趋势相符。
5 结 论
(1)结合平均有效应力的影响,推导出考虑时效性影响的孔隙率和渗透率模型,并利用现场数据对模型有效性进行了验证,确认模型能较好的模拟深部瓦斯长期运移规律。
(2)通过与未考虑时间效应模型的计算结果对比可知,随着抽采过程的进行,考虑时间效应下的孔隙率、渗透率数值明显减小,抽采时间越长,时间效应越明显,考虑时间效应与否的两种模型差值越大。
(3)运用考虑时间效应的渗透率模型分析了瓦斯抽采过程中钻孔周围的渗流场,在本文模拟条件下,当抽采时间为1 d时,临近钻孔中心处渗透率较大、瓦斯压力较小;当抽采时间达到30 d时,模型内渗透率与瓦斯压力的演化趋于平衡状态,临近与远离钻孔中心处的数值差别较小。
[1] 谢和平,周宏伟,薛东杰,等.煤炭深部开采与极限开采深度的研究与思考[J].煤炭学报,2012,37(4):535-542.
XIE Heping,ZHOU Hongwei,XUE Dongjie,et al.Research and consideration on deep coal mining and critical mining depth[J].Journal of China Coal Society,2012,37(4):535-542.
[2] 谢和平,周宏伟,薛东杰,等.我国煤与瓦斯共采:理论、技术与工程[J].煤炭学报,2014,39(8):1391-1397.
XIE Heping,ZHOU Hongwei,XUE Dongjie,et al.Theory,technology and engineering of simultaneous exploitation of coal and gas in China[J].Journal of China Coal Society,2014,39(8):1391-1397.
[3] 谢和平,高峰,周宏伟,等.煤与瓦斯共采中煤层增透率理论与模型研究[J].煤炭学报,2013,38(7):1101-1108.
XIE Heping,GAO Feng,ZHOU Hongwei,et al.On theoretical and modeling approach to mining-enhanced permeability for simultaneous exploitation of coal and gas[J].Journal of China Coal Society,2013,38(7):1101-1108.
[4] 薛东杰,周宏伟,孔琳,等.采动条件下被保护层瓦斯卸压增透机理研究[J].岩土工程学报,2012,34(10):1910-1916.
XUE Dongjie,ZHOU Hongwei,KONG Lin,et al.Mechanism of unloading-induced permeability increment of protected coal seam under mining[J].Chinese Journal of Geotechnical Engineering,2012,34(10):1910-1916.
[5] SEIDLE J P,JEANSONNE M W,ERICKSON D J.Application of matchstick geometry to stress dependent permeability in coals[A].SPE rocky mountain regional meeting[C].Society of Petroleum Engineers,1992:433-444.
[6] PALMER I,MANSOORI J.How permeability depends on stress and pore pressure in coalbeds:A new model[A].SPE Annual Technical Conference and Exhibition[C].Society of Petroleum Engineers,1998:539-544.
[7] SHI J Q,DURUCAN S.Drawdown induced changes in permeability of coalbeds:A New Interpretation of the reservoir response to primary recovery[J].Transport in Porous Media,2004,56(1):1-16.
[8] CUI Xiaojun,BUSTIN R M.Volumetric strain associated with methane desorption and its impact on coalbed gas production from deep coal seams[J].AAPG Bulletin,2005,89(9):1181-1202.
[9] 卢平,朱贵旺.岩样应力应变全程中的渗透性表征与试验研究[J].中国科学技术大学学报,2002,32(6):678-684.
LU Ping,ZHU Guiwang.Characterization of and experimental study on the permeability of rock-samples during complete stress-strain course[J].Journal of University of Science and Technology of China,2002,32(6):678-684.
[10] 周辉,杨艳霜,刘海涛.岩石强度时效性演化模型[J].岩土力学,2014,35(6):1521-1527.
ZHOU Hui,YANG Yanshuang,LIU Haitao.Time-dependent theoretical model of rock strength evolution[J].Rock and Soil Mechanics,2014,35(6):1521-1527.
[11] 周宏伟,王春萍,段志强,等.基于分数阶导数的盐岩流变本构模型[J].中国科学:物理学力学天文学,2012,42(3):310-318.
ZHOU Hongwei,WANG Chunping,DUAN Zhiqiang,et al.Time-based fractional derivative approach to creep constitutive model of salt rock[J].Scientia Sinica Physica,Mechanica & Astronomica,2012,42(3):310-318.
[12] 尹光志,何兵,王浩,等.深部采动影响下覆岩蠕变损伤破坏规律[J].煤炭学报,2015,40(6):1390-1395.
YIN Guangzhi,HE Bing,WANG Hao,et al.Damage law of overlying rock induced by mining[J].Journal of China Coal Society,2015,40(6):1390-1395.
[13] 周长冰,万志军,张源,等.高温三轴应力下气煤蠕变特征及本构模型[J].煤炭学报,2012,37(12):2020-2025.
ZHOU Changbing,WAN Zhijun,ZHANG Yuan,et al.Creep characteristics and constitutive model of gas coal mass under high temperature and triaxial stress[J].Journal of China Coal Society,2012,37(12):2020-2025.
[14] 许江,彭守建,陶云奇,等.蠕变对含瓦斯煤渗透率影响的试验分析[J].岩石力学与工程学报,2009,28(11):2273-2279.
XU Jiang,PENG Shoujian,TAO Yunqi,et al.Experimental analysis of influence of creep on permeability of gas-bering coal[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(11):2273-2279.
[15] 郝富昌,刘彦伟,龙威成,等.蠕变-渗流耦合作用下不同埋深有效抽采半径研究[J].煤炭学报,2017,42(10):2616-2622.
HAO Fuchang,LIU Yanwei,LONG Weicheng,et al.Effective gas extraction radius of different burial depths under creep-seepage coupling[J].Journal of China Coal Society,2017,42(10):2616-2622.
[16] NISHIHARA M.Creep of shale and sandy-shale[J].The Journal of the Geological Society of Japan,1952,58(683):373-377.
[17] JAEGER J C,COOK N G W,ZIMMERMAN R.Fundamentals of rock mechanics[M].John Wiley & Sons,2009:169-204.
[18] CUI Xiaojun,BUSTIN R M,CHIKATAMARLA LAXMI.Adsorption-induced coal swelling and stress:Implications for methane production and acid gas sequestration into coal seams[J].Journal of Geophysical Research,2007,112(B10202).
[19] DANESH N N,CHEN Z,AMINOSSADATI S M,et al.Impact of creep on the evolution of coal permeability and gas drainage performance[J].Journal of Natural Gas Science and Engineering,2016,33:469-482.
[20] 范超军,李胜,罗明坤,等.基于流-固-热耦合的深部煤层气抽采数值模拟[J].煤炭学报,2016,41(12):3076-3085.
FAN Chaojun,LI Sheng,LUO Mingkun,et al.Deep CBM extraction numerical simulation based on hydraulic-mechanical-thermal coupled model[J].Journal of China Coal Society,2016,41(12):3076-3085.
[21] SHI J Q,DURUCAN S.Exponential growth in San Juan basin Fruitland coalbed permeability with reservoir drawdown:Model match and new insights[J].SPE Reservoir Evaluation and Engineering,2010,13(6):914-925.
