

中国是煤炭生产和消费大国,每年消耗煤炭近40亿t,占到我国一次能源供应的60%。然而煤炭在开发利用过程中会引起地下水、大气等环境污染,我国目前有近70万台中小型燃煤锅炉,年消耗煤约6~8亿t,这是导致国内雾霾问题的首要来源[1]。这些小中型锅炉很多使用劣质烟煤,而这种灰分很高的煤(大于40%)单位质量燃烧污染物相当于电煤的5~10倍[2]。随着优质开采煤比例的下降,降低劣质煤灰分,转化为优质煤是一种必然路径。
煤中的无机灰分以微米级粒度和复杂多样的状态嵌布在有机碳质中,因此只有当颗粒粉碎到一定细度时,才能使灰分与碳质发生充分解离,然后通过后续的分选手段,比如油聚团使煤-灰分别聚团,再利用浮选技术将煤-灰分开[3] 等手段,获得低灰分的洁净煤。由于煤-矸石的嵌布状态和粉碎后表面性质的巨大差异,不同的煤为达到要求的煤-矸石解离度所需要的粒度分布是不同的,付晓恒等[4]提出,当粒度破碎到10 μm以下时,大多数的煤和无机矿物已经获得比较充分的解离。但王捷[3] 经试验验证,淮南煤在粉碎至5 μm时,仍有黏土矿物没有得到充分解离。矿物提质前的颗粒粉碎过程是一个高耗能的过程,通常占到整个矿物加工的30%~70%。基于对颗粒破碎过程主要矛盾的假设,能耗理论有经典的三大假说,即体积假说[5]、裂缝假说[6]和面积假说[7],分别描述物料的粗碎、中碎和细碎阶段。其中基于面积假说的Rittinger理论认为外界输入的能量全部用于物料比表面积的增加,尤其适用于<200 μm的细碎过程,而Tomoyoshi在面积假说的基础上考虑到物料越细时越难粉碎、单位能量产生的新表面积越小的事实,认为比表面积增量对功耗增量的比与极限比表面积与瞬时比表面积的差成正比,如式(1),(2)所示,s 为极限比表面积,与粉碎物料性质和研磨设备相关;s为瞬时比表面积;K为常数;sf为进料比表面积;sp为出料比表面积;e为粉碎能耗。
为极限比表面积,与粉碎物料性质和研磨设备相关;s为瞬时比表面积;K为常数;sf为进料比表面积;sp为出料比表面积;e为粉碎能耗。
(1)
![]()
(2)
表征物料粒度分布的Rosin-Rammler(R-R)粒度分布模型[8]和Gates-Gaudin-Schuhmann(GGS)粒度分布模型[9]经常用来建立研磨出料的粒度分布与研磨能耗的关系式[10-11],最近分形理论应用于超细研磨也取得了不少进展,例如,杨致远等[12]结合分形理论,分析了球磨机超细研磨过程;曾凡桂[13]借助分形理论建立了煤粉碎动力学方程,对6种不同变质程度的煤进行了动力学分析并获得了其粉碎动力学参数。
最近不断发展的基于物料破碎机理的动力学模型由于包含了磨机研磨中的物理过程,因而对研磨过程的优化、研磨能耗效率、对出料粒度的控制具有非常大的意义和价值。矩阵模型(Matrix Model)将整个破碎过程看作是重复的破碎事件的累加;粒群平衡模型(Population Balance Model,PBM)将破碎过程看作是时间上的连续过程,并且可以考察破碎物料性质和磨机的操作条件(磨介尺寸,转轴速度等)对于物料破碎的影响。 PETRAKIS等[14]借助PBM模型对球磨机粉碎石英的过程进行了优化,获得了球磨机的钢球填充率与破碎速率的关系曲线。2017年PETRAKIS和KOMNITSAS[15]将BROADBENT和CALLCOTT[16]提出的矩阵模型和PBM模型[17]相结合,用来预测球磨机在毫米级入料的干法研磨出料粒度分布,取得了较好的模拟结果,这种方法是基于颗粒破碎的一阶线性动力学假设[18]。这里我们称之为矩阵粒群平衡模型(Matrix Population Balance Model,M-PBM模型),将其拓展应用于立式搅拌磨机的湿法超细研磨过程,此方法是将物料破碎看作是一连串衔接的破碎事件的组合,每一个“基元”破碎事件的入料,就是上一个“基元”破碎事件的出料,破碎时间越久,重复的“基元”破碎次数就越多。入料和出料的粒度分布由n个等比例缩减的筛网尺寸划定的n个离散的粒度区间(discrete-size classes)来表示,第i个粒度区间内颗粒的粒径用区间顶端的筛网尺寸,即第i个筛网尺寸代表。描述每个粒度区间内颗粒的破碎概率用选择破碎函数Si(min-1)表示:
(3)
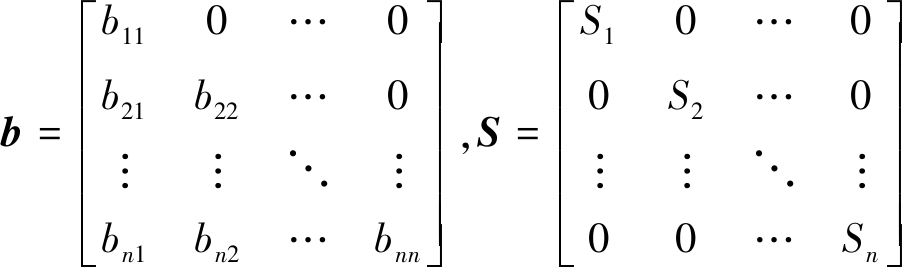
其中,Si为单位时间内位于粒度区间i的颗粒群在一次‘基元’破碎事件中发生破碎的比例,其大小随着颗粒大小不同可能不同;αT和θ为与物料性质和磨机操作条件相关的参数[19];x0为标准尺寸1 mm;xi的单位是mm。每个粒度区间内颗粒破碎后的子颗粒分配到其他粒度区间的过程用破碎函数bij(i>j)表示,比如b21代表位于第1个粒度区间内破碎的颗粒落到第2个更细粒度区间的颗粒占1区间总破碎颗粒的比例,破碎函数bij通常用累积破碎函数Bij(i>j)来表示(式(4),γ为与物料性质相关的参数),比如B31表示粒度区间1中的颗粒破碎后,子颗粒落到第3个粒度区间及以下的比例;假设一个破碎过程由u个“基元”破碎事件组成,那么最终破碎过程的入料和出料的关系就可以用式(5)来描述,其中S为选择破碎函数对角矩阵(n×n);b为破碎函数下三角矩阵(n×n);I为单位矩阵(n×n);f和p分别为入料和出料的粒度分布向量(n×1);Δt为每个“基元”步骤经历的研磨时间;u为研磨经过的“基元”步骤次数。
(4)
p=(bSΔt+I-SΔt)uf
(5)

为了回归M-PBM模型中的参数以便对磨机的出料粒度分布进行模拟,笔者借助Matlab编写了一套程序代码,步骤如下:
首先确定n个粒度区间,用来划分实验得到的进料f的颗粒群的粒度分布,相邻粒度区间粒径比1.098,与激光粒度仪的粒度区间表示相同。
由式(3)和(4)计算各个粒度区间的Si和bij,构建S和b矩阵(带有αT,θ和γ未知参数),每个“基元”研磨步的时间Δt取值1/3 min。
由式(5)计算经过u个“基元”研磨步骤后的出料粒度p(带有αT,θ和γ未知参数)。
借助Matlab中的fmincon函数对目标函数Fun(式(6))进行最优化,其中![]() 和
和![]() 分别为经过t个“基元”破碎步骤后,至粒度区间i的筛下累积百分含量的M-PBM模型计算值和实验值。通过寻找最优的αT,θ和γ,使得实验值和模拟值的误差最小。
分别为经过t个“基元”破碎步骤后,至粒度区间i的筛下累积百分含量的M-PBM模型计算值和实验值。通过寻找最优的αT,θ和γ,使得实验值和模拟值的误差最小。
(6)
αT,θ和γ确定后,即可通过式(3)和(4)构建b和S数值矩阵,最后通过(5)来求出任意研磨步骤的出料粒度分布p。
试样分别选取太西煤、锦丘煤和金达煤,其中太西煤灰分最低,色泽乌黑亮丽。锦丘煤和金达煤的色泽灰暗程度依次升高,灰分最高的金达煤色泽明显呈灰黑色(表1)。
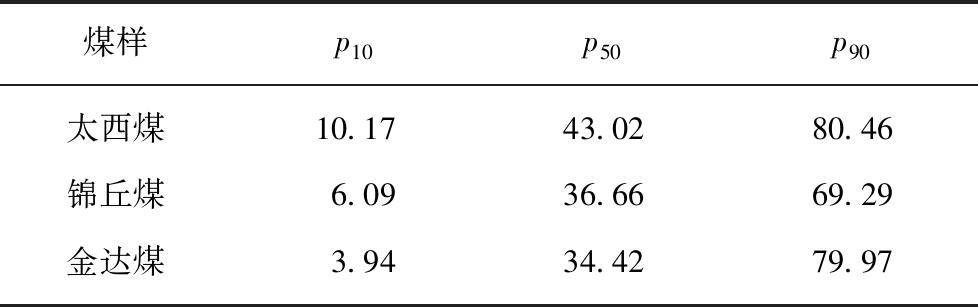
3种煤样各取100 kg,采用圆锥1/4取样法,获得性质均一的煤样各6 kg。首先用对辊机将煤样破碎到0.5 mm以下,然后用球磨机研磨35 min,球磨机出料用75 μm筛子干筛,取75 μm筛下物作为搅拌磨机入料。3种煤样的粒度分布见表2。
表1 3种煤样的工业分析
Table 1 Industrial analysis of the three coal samples %

煤样MadAadAdVadVdVdafFadFCd太西煤0.6203.0103.0277.4777.5237.75788.89389.450锦丘煤2.89326.63027.42332.05333.01045.48738.42339.567金达煤3.58349.38351.21722.37323.20347.60324.66025.573
表2 球磨机出料的筛下累积粒度分布
Table 2 Accumulative particle size distributions under sieve of grinding product by ball mill μm
煤样p10p50p90太西煤10.1743.0280.46锦丘煤6.0936.6669.29金达煤3.9434.4279.97
本实验使用装置为带有冷却水夹套的1.5 L立式搅拌磨机,搅拌电机额定功率750 W。如图1所示,研磨筒体直径100 mm,高度300 mm,研磨筒体内填装3.7 kg高铝氧化铝陶瓷球(Al2O3≥92%)。实验前,先将特定质量比例的煤粉和水混合,加入研磨分散剂六偏磷酸钠(煤粉质量的0.5%),然后用高速分散仪在50 240 rad/min下分散5 min制成均一的料浆。为使加入研磨筒体内的料浆和磨球在研磨开始后尽快达到均匀混合状态,加料时采用磨球和料浆交替层层加入的方式。根据GUPTA[20]对于研磨动力学中入料的建议,同时也为避免由于初始搅拌不均造成的采样数据异常,以研磨开始后的40 s取样样品作为0时刻的粒度分布。研磨过程中,磨球在搅拌转轴的搅拌下做螺旋式自上而下快速循环运动,可以认为研磨桶内的料浆处于全混状态。使用秒表记录研磨时间,在特定时间点用针管取样器从料浆上部取样用于粒度分析,使用功率计测定实时功率,通过转速计反馈实时搅拌转速,整个过程的转速控制在9 420 rad/min左右。

图1 1.5 L立式搅拌球磨机
Fig.1 1.5 L vertical stirred ball mill
此外,本实验使用仪器为美国Beckman公司生产的LS13320型激光粒度测试仪检测不同研磨时间点的料浆的粒度分布,方法采用湿法检测,煤的折射指数实部设定为1.8,虚部设定为0.8。
根据田口(Taguchi)三因素三水平正交实验表进行实验设计,实验考察3个因素:比处理量(煤质量/磨介质量,其中磨介质量固定在3.7 kg),磨介尺寸,不同灰分的煤种(表3)。
表3 田口(Taguchi)正交实验
Table 3 Taguchi experimental plan

实验编号比处理量/(kg·kg-1)磨介尺寸/mm灰分/%10.0701.849.420.0820.849.430.1010.349.440.0821.83.050.1010.83.060.0700.33.070.1011.826.680.0700.826.690.0820.326.6
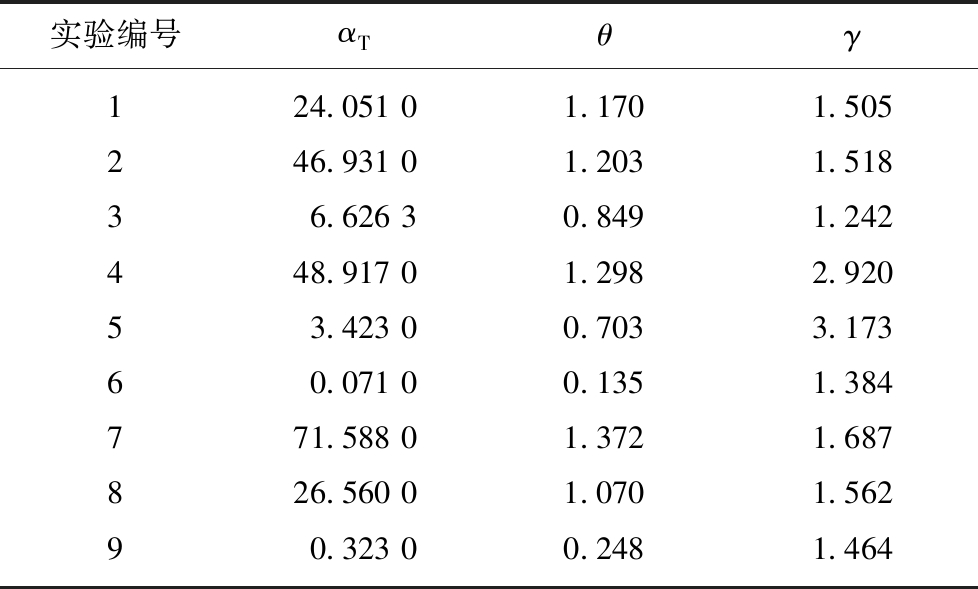
为了图表简洁,这里只展示了使用1.8 mm磨介的3组出料粒度分布的实验和模拟值,其他0.8和0.3 mm磨介效果与1.8 mm磨介模拟结果无明显区别(R2均大于0.9),表4为基于9组正交实验回归得到的M-PBM参数,将这些参数代入到式(3)~(5)即可由已知的入料f计算出某一时刻的出料p。图2分别为金达煤、太西煤和锦丘煤的粒度分布随时间变化的实验值和模拟值,虽然3种煤的灰分差别较大(表1),3组实验的比处理量也不同(表3),但是采用M-PBM方法能够非常精确的预测粒度分布随时间的变化情况(表4),说明此方法完全可以应用于立式搅拌球磨机湿法超细研磨的粒度分布预测。

图2 实验检测和M-PBM模拟的不同时间点的产品粒度分布
Fig.2 Experimental and M-PBM simulated particle size distributions at various time points
表4 正交实验的M-PBM回归参数
Table 4 M-PBM regression parameters from Taguchi experiments
实验编号αTθγ124.051 01.1701.505246.931 01.2031.51836.626 30.8491.242448.917 01.2982.92053.423 00.7033.17360.071 00.1351.384771.588 01.3721.687826.560 01.0701.56290.323 00.2481.464
由于M-PBM模拟得到的粒度分布中,将连续的颗粒粒径的变化分割为几个离散的粒度区间,比如一般的筛分实验中相邻筛网尺寸比是1.414,这样相邻粒度区间的累积百分含量的变化有时非常大(20%~30%),因此为了更加准确而方便地确定任意累积百分含量下的颗粒粒径,更精确地预测出料粒度分布,这里我们引入Rosin-Rammler粒度分布模型(R-R模型),R-R模型经常用来拟合物料的累积粒度分布,式(7)所示,px为筛下累积百分含量;x为粒径;α和b为常数。
(7)
式(7)两边取自然对数,可以得到
(8)
借助M-PBM模拟的累积粒度分布px数据,将式(8)左边项对ln x作线性回归,可得到斜率α和b,最后计算任一筛下累积分率的粒径x。然而有些情况下R-R分布模型或GGS模型无法完全准确描述整个出料粒度范围内的分布情况。因而PETRAKIS等[21]提出了分段回归(piece-wise regression)策略,即将粒度区间分为两部分,对每一部分依据式(8)分别做线性回归,得到2套参数(α1,b1和α2,b2)用来分别拟合两段粒度区间的粒度分布。借助上述方法,我们可以精确地确定M-PBM模拟的任意筛下累积粒度分布对应的粒径x,这里以筛下累积含量50%p50对应的粒径x为参照与激光粒度分析仪测得的x(p50)进行对比。基于表3所示的9组实验,每组实验在6个不同的时间点取样(20,140,320,500,680,860)s,共54套PSD数据计算了p50对应的粒度x,见表5(用筛下累积分布50%对应的粒度进行对比),M-PBM和R-R粒度分布模型得到的p50粒度与激光粒度分析仪的实验值符合非常好。
表5 1.8,0.8,0.3 mm磨介实验测量与M-PBM+R-R粒度分布模型模拟
Table 5 1.8,0.8,0.3 mm grinding media experimental measured and M-PBM+R-R distribution model simulated data μm

粒度/mm实验编号研磨时间/s0201403205006808601-Exp-p5010.249.097.215.714.824.303.961-PBM-p5010.249.037.265.754.814.173.691.84-Exp-p5022.0719.4115.4111.199.488.107.494-PBM-p5022.0721.2415.8612.099.948.567.527-Exp-p5018.4415.9010.707.555.845.044.517-PBM-p5018.4414.579.837.155.784.934.332-Exp-p5012.5010.047.084.283.413.032.692-PBM-p5012.5010.497.175.134.083.412.940.85-Exp-p5027.8325.8621.5116.2812.9610.749.305-PBM-p5027.8324.9120.9716.7913.8811.6810.028-Exp-p5021.5617.379.926.394.734.073.498-PBM-p5021.5616.7910.106.534.873.903.253-Exp-p509.428.165.964.583.723.042.703-PBM-p509.429.487.155.184.023.272.740.36-Exp-p5024.7623.8821.0019.3518.6217.8817.646-PBM-p5024.7622.7221.3519.4817.8116.3014.959-Exp-p5016.7113.3110.309.076.666.005.309-PBM-p5016.7114.6212.5610.148.196.665.45
2.3.1 磨机能耗和通量计算
一般颗粒粒度在1~10 μm内的粉体称为微米级超细粉体。这里根据磨机的研磨粒度下限,对10~3 μm的粒度变化区间的研磨能耗和磨机的研磨通量进行考察。M-PBM+R-R粒度分布模型可以精确地确定任意研磨时刻下任一筛下累积百分含量px对应的颗粒直径x。这里根据研磨实验粒度变化的上下限,考察了10 μm(p50)~3 μm(p50)粒度变化区间的煤粉从0时刻初始粒径分别减小到10 μm(p50)的时间t1(s)和减小到3 μm(p50)的时间t2(s),那么研磨时间为t2(s)-t1(s),功率P已由功率计测得,则研磨的能耗(单位质量煤粉的耗电量,kW·h/kg)和比通量(单位时间单位质量磨介煤粉的处理量,kg/(kg·h))就可通过上述物理量计算得出。表6显示了正交实验9组设计实验,其10 μm(p50)~3 μm(p50)的研磨时间、比通量和能耗。可以明显地发现4~6组实验(太西煤)的研磨时间明显大于金达煤(1~3组实验)和锦丘煤(7~9组实验),研磨能耗也明显偏高。第3组金达煤的比通量最高,研磨能耗最低。
表6 正交实验的研磨通量和研磨能耗
Table 6 Specific flux and energy consumption results

实验标号时间/min比通量/(kg·(kg·h)-1)研磨能耗/(kW·h·kg-1)120.70.204 00.414213.70.361 00.231312.70.479 00.152450.00.098 90.781534.70.175 00.439646.30.091 10.709724.00.253 00.332813.70.308 00.259918.00.275 00.293
2.3.2 研磨通量和能耗的极差分析
煤颗粒中的无机矿物(灰分)以微米级细度嵌布于有机碳质中,由于灰分和有机碳质元素组成差异和力学性质不同,不同的灰分会引起煤颗粒断裂韧性、杨氏弹性模量和受力时内部裂纹扩展[22]的差异,从而影响颗粒的破碎速率。此外磨机的研磨性能与操作条件息息相关,比如料浆浓度、磨介尺寸、研磨分散剂用量和转轴转速等。
此处为了更好的突出磨介尺寸、比处理量和煤自身性质(灰分)对于研磨通量和能耗的影响大小,使用极差分析(range analysis)的方法对上述因素进行了分析,由表7可知对研磨通量影响最大的是煤的灰分,与比通量呈现正相关性;比处理量和磨介尺寸对研磨通量的影响无太大差别。研磨能耗受灰分的影响很明显,且呈负相关性,磨介尺寸影响次之,比处理量最小。太西煤最难磨,其他两种煤的能耗平均不到太西煤的一半。
表7 研磨通量和研磨能耗的极差分析
Table 7 Range analysis for specific flux and energy consumption

考察因素考察水平比通量/(kg·(kg·h)-1)研磨能耗/(kW·h·kg-1)比处理量/0.0700.2010.461(kg·kg-1)0.0820.2450.4350.1010.3020.308变化0.1010.1531.80.1850.509磨介尺寸/mm0.80.2810.3100.30.2820.385变化0.0970.1993.00.1220.643灰分/%26.60.2790.29549.40.3480.266变化0.2260.377
2.3.3 研磨能耗和通量模型
由前面的极差分析可知煤的灰分对磨机的能耗和通量影响最明显,这里我们借助Tomoyoshi的能耗-比表面积关系式来探讨灰分与能耗之间的内在关联。由式(2)可知,随着颗粒研磨过程中粒度dp不断减小,物料的比表面积(∝1/dp)会迅速增大,最后趋近物料研磨的极限比表面积s ,煤颗粒在破碎过程中嵌布其中的微米级灰颗粒会不断解离,由于灰分和有机碳质元素组成差异和力学性质不同,不同灰分的煤的s
,煤颗粒在破碎过程中嵌布其中的微米级灰颗粒会不断解离,由于灰分和有机碳质元素组成差异和力学性质不同,不同灰分的煤的s 是不同的。研磨出料可以认为是由解离的灰颗粒、解离不充分的煤-灰颗粒和解离完全的煤颗粒构成的,付晓桓等[4]的研究指出当粒度破碎到10 μm以下时,大多数的煤和无机矿物已经获得比较充分的解离,王捷[3] 的实验发现太西煤破碎到15 μm时,无机矿物已得到较为充分的解离。本实验考察的能耗对应的研磨粒度区间是[3,10]μm,可以认为煤-灰解离充分,因此可以认为物料由解离完全的灰和解离完全的煤颗粒构成。那么将s
是不同的。研磨出料可以认为是由解离的灰颗粒、解离不充分的煤-灰颗粒和解离完全的煤颗粒构成的,付晓桓等[4]的研究指出当粒度破碎到10 μm以下时,大多数的煤和无机矿物已经获得比较充分的解离,王捷[3] 的实验发现太西煤破碎到15 μm时,无机矿物已得到较为充分的解离。本实验考察的能耗对应的研磨粒度区间是[3,10]μm,可以认为煤-灰解离充分,因此可以认为物料由解离完全的灰和解离完全的煤颗粒构成。那么将s =Ads
=Ads ,A+(1-Ad)s
,A+(1-Ad)s ,C,其中s
,C,其中s ,A和s
,A和s ,C分别为完全解离的灰和完全解离的煤的研磨极限比表面积,代入式(2)并整理可得
,C分别为完全解离的灰和完全解离的煤的研磨极限比表面积,代入式(2)并整理可得
(9)
表6所示的9组实验的研磨能耗对应的粒度变化区间为[3,10] μm,故进料比表面积sf和出料比表面积sp是常数,1/K可以看作是功耗系数,这里假定功耗系数与灰分Ad和灰的功耗系数1/KA和煤的功耗系数1/KC的关系为1/K=(1/KA)Ad+(1/KC)(1-Ad),结合式(9),研磨能耗与灰分的关系为
(10)
LI等[23]实验研究指出Netzsch卧式搅拌磨机的能耗与比处理量的对数成正比,与磨介尺寸的幂函数成正比。这里我们使用的1.5 L搅拌磨机内填充的陶瓷球(堆密度2.2 kg/L)的床层高度只有250 mm,在转轴高速搅拌状态下其重力对其磨介流动的影响比工业大型立式搅拌磨机小的多,这里我们提出一个研磨能耗E的回归模型(式(11)),考虑了磨机的比处理量L、磨介尺寸M和灰分Ad三种因素的影响。
a6ln L+a7M3
(11)
式中,a1=-3.100;a2=-0.618;a3=2.011;a4=2.265;a5=0.651;a6=-0.427;a7 =0.028。
拟合值与实验值的R2 =0.952。可知在超细粉磨粒度范围内,煤的灰分越高能耗越低;同时磨介尺寸越小,能耗越小;比处理量越大,能耗越小。搅拌磨机的比通量Q的模型与能耗模型类似:
a12+a13ln L+a14M3
(12)
式中,a8=0.428,a9=2.293,a10=0.808,a11=28.630,a12=0.731,a13=0.276,a14=-0.017。
拟合值与实验值的R2 =0.920。可知在超细粉磨粒度范围内,煤的灰分越高比通量越高;同时磨介尺寸越小,比通量越高;磨机的比处理量越大,比通量越高。

图3 研磨能耗E的实验值和预测值
Fig.3 Experimental and predicted grinding energy consumption
图3(a)为式(10)计算得到的预测值和实验值,图3(b)为式(11)计算得到的预测值和实验值,可以看到预测值和实验值的吻合度较高。
本次研究中,我们在间歇立式搅拌磨机的特定转速下,重点考察了性质不同的3种煤在不同的物料比处理量、不同的磨介尺寸和1~10 μm微米级超细粉体范围内的研磨动力学和能耗特征,构建的M-PBM结合R-R粒度模型能够精确地预测上述各种不同工况下的粒度分布。除了上述影响因素外,必须指出的是磨机的转轴转速对物料的粉碎过程具有非常重要的影响,一般来说转速越高,磨介在筒体中整个的循环流动速度会越大,磨介球之间的剪切强度会更高,从而加速物料的粉碎,但转速越高消耗的功率也会越高,因此磨机的转速有一个最优值。不同尺寸磨介的研磨性能与物料的粒度大小是相关的,磨介尺寸不同其发挥最优研磨性能对应的物料粒度区间是不同的,一般来说,磨介尺寸越小其发挥高效研磨的物料粒度区间上下限会同时减小,反之亦然。因此对于特定的研磨粒度区间,需要匹配合适尺寸的研磨介质。由于篇幅限制,我们暂时没能对上述因素进行深入考察,但是搅拌轴转速的影响以及研磨介质尺寸和物料粒度的匹配对研磨动力学和能耗的影响是我们下一步一个重要的研究方向之一。
(1)基于田口正交实验设计,考察了1.5 L立式搅拌磨机不同比处理量、不同磨介尺寸和不同灰分的煤粉的湿法超细研磨过程,应用矩阵粒群平衡模型(Matrix Population Balance Model,M-PBM)对上述各种不同工况下,不同灰分的煤的出料粒度分布进行模拟,发现一阶线性动力学的假设就可以很好地应用于搅拌磨机超细研磨的出料粒度模拟,为煤粉的湿法超细研磨过程奠定实验和理论基础。
(2)使用M-PBM预测出的离散的粒度分布数据,再结合分段Rosin-Rammler 粒度分布模型,精确地预测了任意累积百分含量下的颗粒粒度,M-PBM+R-R粒度模型可应用于不同灰分的煤粉的超细研磨的粒度分布预测。
(3)对研磨比通量和能耗的极差分析可知,在定搅拌转轴转速和所考查的研磨粒度变化范围内,煤的灰分对搅拌磨机的比通量和能耗的影响是最大的。
(4)基于对煤粉超细研磨过程中煤-灰解离过程的分析,并结合Tomoyoshi的比表面积能耗公式,探讨了煤的灰分与能耗的关系,建立了研磨能耗E(kW·h/kg)和比通量Q(kg/(kg·h))与比处理量L(kg/kg)、灰分Ad(%)和磨介尺寸M(mm)的函数关系式,在10 μm(p50)以下的超细粉磨粒度范围内,煤的研磨能耗随着灰分的提高、磨介尺寸的减小(磨介尺寸在0.3~1.8 mm)和比处理量的增大而减小;而比通量随着灰分的提高、磨介尺寸的减小和比处理量的增大而增大。
[1] 中国电力企业联合会.2016年全国电力工业统计快报数据一览表[DB/OL].www.cec.org.cn,2017-01-13.
[2] 刘科.治霾先治散烧煤和柴油机[N/OL].www.huanqiu.com,2015-04-18.
LIU Ke.Combustion of scattered coal and emissions of diesel engine are the starting points for solving haze problems[N/OL].www.huanqiu.com,2015-04-18.
[3] 王婕.超细粉碎颗粒性质对超净煤分选的影响[D].北京:中国矿业大学(北京),2016.
WANG Jie.Effect of ultra-fine particle properties on the separation of ultra-clean coal[D].Beijing:China University of Mining & Technology(Beijing),2016.
[4] 付晓恒,李萍,刘虎,等.煤的超细粉碎与超净煤的分选[J].煤炭学报,2005,30(2):219-223.
FU Xiaoheng,LI Ping,LIU Hu,et al.Ultra-fine grinding of coal and preparation of ultra-clean coal[J].Journal of China Coal Society,2005,30(2):219-223.
[5] KICK F,GESETZ D.Proportionalen widerstände und seine anwendungen[M].Leipzig:Felix,1885.
[6] BOND F C.The third theory of comminution[J].Transactions of the American Institute of Mining and Metallurgical Engineers,1952,193:484-494.
[7] RITTINGER P R.Lehrbuch a[M].Berlin:Ernst & Korn,1867:47.
[8] ALLEN T.Powder sampling and particle size determination[M].Amsterdam:Elsevier,2003.
[9] KING R P.Modeling and simulation of mineral processing systems[M].Oxford:Butterworth-Heinemann,2001.
[10] STAMBOLIADIS E T.A contribution to the relationship of energy and particle size in the comminution of brittle particulate materials[J].Minerals Engineering,2002,15(10):707-713.
[11] STAMBOLIADIS E T.The relationship of energy and particle size in comminution[J].Mining and Metallurgical Annals,1996,6(2):9-21.
[12] 杨志远,曲建林,周安宁.超细煤粉颗粒形状分形维数与球磨工艺的研究[J].煤炭学报,2004,29(3):342-345.
YANG Zhiyuan,QU Jianlin,ZHOU Anning.Study on the relationships between the profile fractal dimensions of coal ultra-fine powders and their grinding technologies[J].Journal of China Coal Society,2004,29(3):342-345.
[13] 曾凡桂.用粒度表征的煤粉碎动力学方程[J].煤炭学报,2000,25(3):303-306.
ZENG Fangui.Coal crushing kinetics equation described by particle size[J].Journal of China Coal Society,2000,25(3):303-306.
[14] PETRAKIS E,STAMBOLIADIS E T,KOMNITSAS K.Indentification of optimal mill operating parameters during grinding of quartz with the use of population balance model[J].Kona Powder and Particle Journal,2017,34:213-223.
[15] PETRAKIS E,KOMNITSAS K.Improved modeling of the grinding process through the combined use of matrix and population balance models[J].Minerals,2017,7(5):67.
[16] BROADBENT S R,CALLCOTT T G.A matrix analysis of processes involving particle assemblies[J].Philosophical Transactions of the Royal Society A Mathematical Physical & Engineering Sciences,1956,249(960):99-123.
[17] RAMKRISHNA D,SINGH M R.Population balance modeling:Current status and future prospects[J].The Annual Review of Chemical and Biomolecular Engineering,2014,5(8):123-146.
[18] BILGILI E,SCARLETT B.Population balance modeling of non-linear effects in milling processes[J].Powder Technology,2005,153:59-71.
[19] NOMURA S,HOSODA K,TANAKA T.An analysis of the selection function for mills using balls as grinding media[J].Powder Technology,1991,68:1-12.
[20] GUPTA V K.Determination of the specific breakage rate parameters using the top-size-fraction method:Preparation of the feed charge and design of experiments[J].Advanced Powder Technology,2016,27:1710-1718.
[21] PETRAKIS E,STAMBOLIADIS E T,KOMNITSAS K.Evaluation of the relationship between energy input and particle size distribution in comminution with the use of piecewise regression analysis[J].Particulate Science and Technology,2017,35(4):479-489.
[22] 江山,方嵋,殷秋生,等.颗粒粉碎能耗与粒度的关系[J].北京科技大学学报,1996,18(2):112-116.
JIANG Shan,FANG Mei,YIN Qiusheng,et al.Relationship between energy consumption and particle size in comminution[J].Journal of University of Science and Technology Beijing,1996,18(2):112-116.
[23] LI H,NDJAMO A,SAURIOL P,et al.Optimization of LiFePO4 wet media milling and regressive population balance modeling[J].Advanced Powder Technology,2017,28:1000-1007.