煤矿井筒经常穿越富水软弱砂层,在井筒建设及使用过程中极易诱发涌水溃砂灾害[1],严重威胁煤矿的安全生产。注浆[2-4]作为加固砂层的有效手段,在煤矿井筒穿越砂层段治理中获得了广泛应用,大量砂层注浆工程实践表明,劈裂-压密注浆模式[5-6]是砂层注浆工程中的主要模式。
砂层劈裂-压密注浆扩散过程是浆液流场与砂层应力场相互耦合的过程,其中,砂层应力变形过程由砂层自身压密特性所控制,浆液流动由浆液自身本构流型控制,在注浆结束后,形成由浆脉骨架及被压密砂层所组成的复合体,在浆脉骨架支撑与砂层压密固结的协同作用下,砂层整体性能得到提高。
相关学者针对劈裂-压密注浆扩散理论进行了诸多研究,邹金峰等[7]、孙锋等[8-9]、张忠苗等[10]基于平板窄缝模型,分别将浆液视为牛顿流体、宾汉流体及幂律流体,建立了相应的劈裂注浆扩散方程,但是上述研究中均假设劈裂通道开度恒定不变,没有考虑浆液压力对地层的压密作用及压密后地层对注浆扩散过程的影响。在后续研究中,张庆松等[5]考虑了劈裂注浆过程中浆液对劈裂通道两侧地层的压密效应,认为地层压密过程符合温克尔弹性地基梁模型[11],建立了基于“浆-土”界面应力耦合效应的劈裂注浆理论模型;在此基础上,张连震等[12]将土体压密过程的非线性效应引入劈裂注浆扩散过程的研究中,利用初始压缩量Es0及特征压缩模量Es1-2两个常规的地勘试验参数建立了可描述土体非线性压密过程的数学模型,并分析了不同Es0,Es1-2对劈裂注浆扩散过程的影响。然而,由于黏土与砂层在压密特性上具有明显差别,该压密数学模型并不能很好描述砂层压密特性,另外,该压密数学模型只适用于较低压力范围(<0.5 MPa),与实际劈裂注浆的压力范围有较大差距。综上,目前关于劈裂-压密注浆扩散理论的研究尚不能很好地适用于砂层,在砂层压密特性及其对劈裂-压密注浆扩散过程的影响方面亟需开展相关研究。
笔者从砂层自身压密特性及其对劈裂-压密注浆扩散过程的影响方面开展研究,以山东青岛地区含黏性土砂层为典型砂层介质,通过室内试验测试了不同黏性土含量及初始含水率条件下的砂层压缩变形曲线,从是否形成砂骨架的角度揭示了砂层压密变形机理,并建立了可描述砂层非线性压密过程的数学模型,在此基础上分析了黏性土含量对砂层劈裂-压密注浆扩散过程的影响。
1 砂层劈裂-压密注浆扩散过程分析
砂层劈裂-压密注浆扩散过程是浆液在注浆压力作用下劈开砂层并使劈裂通道不断扩展的动态过程,在劈裂通道形成后浆液在劈裂通道内由注浆孔不断向起劈位置运移,如图1所示,浆液沿着垂直于小主应力的方向发生劈裂并扩展,浆液扩散形态可看做一个与小主应力方向相垂直的“圆饼”形态。

图1 砂层劈裂-压密注浆扩散过程示意
Fig.1 Fracture-compaction grouting diffusion in sand
砂层劈裂-压密注浆扩散过程是浆液流场与砂层应力变形场相互耦合的过程,在劈裂通道扩展过程中,浆液流动造成沿劈裂通道扩展方向的压力沿程下降,劈裂通道各个位置处的浆液压力作用于劈裂通道两侧砂层,在注浆影响范围内的砂层发生压缩变形,进而相应位置处的劈裂通道开度发生变化,导致劈裂通道对浆液扩散的阻力发生改变,反过来又影响浆液流动。
砂层压缩变形过程由砂层本身的压密特性所决定,因此砂层压密特性对砂层劈裂-压密注浆扩散过程会产生影响,相关土力学研究[13]表明,砂层黏性土含量及含水率对砂层压密特性具有显著影响,且砂层压缩过程呈现显著的非线性特征(图2),随着砂层压缩变形量的增大,砂层被压缩的难度不断增加,即砂层压缩模量在发生压缩变形后得到提高。

图2 砂层非线性压缩过程ε-p曲线
Fig.2 ε-p curve of sand soil nonlinear compression process
2 砂层压密特性室内试验
2.1 试验材料、试验仪器及试验方法
笔者依托青岛地铁某区段砂层注浆加固工程,选取该区段含黏性土砂层(图3)作为代表性地层,在该砂层试样的基础上通过调整黏性土含量及初始含水率制作不同重塑砂土试样,进行侧限条件下的标准固结试验,试验方法依据GB/T 50123—1999[14],试样直径为61.8 mm,高度20 mm。实际工程中砂层渗透性较好,在砂层压密过程中孔隙水可以快速排出,为尽可能与实际条件保持一致,设定本文固结试验为完全排水条件,砂层固结过程中的水分可通过透水石直接排出。

图3 青岛地区含黏性土砂层现场照片
Fig.3 Photo of the clayey sand in Qingdao
青岛地区含黏性土砂层试样实测含水率为20.2%,黏性土含量为14.91%,控制粒径d60=1.75 mm,有效粒径d10=0.043 mm,d30=0.45 mm,不均匀系数Cu=40.7,曲率系数Cc=2.69,为级配良好的含细粒土砂[14],砂层试样各粒组质量分数见表1。取青岛地区含黏性土砂层试样中的黏性土成分进行液塑限测试,黏性土液限ωl=32%,塑限ωp=14%,为低液限黏土[14],通过击实试验获得黏性土击实最优含水率为15%,最大干密度为1.798 g/cm3。
表1 砂层试样各粒组质量分数
Table 1 Mass fraction of each grain group in sand layer

粒径/mm<0.075 0.075~0.1600.160~0.3150.315~0.6300.63~1.251.25~2.502.5~5.05~10质量分数/%14.913.507.278.4314.8622.3322.536.17
侧限压缩试验测试仪器采用南京土壤仪器厂生产的WG型单联高压固结仪,根据砂层注浆工程经验,砂层注浆最高压力一般不超过2 MPa,因此,确定施加荷载等级为:50,100,200,300,500,800,1 200,2 000 kPa。每级荷载对应的变形稳定标准为每小时变形量不超过0.005 mm。
由于砂层黏性土含量及初始含水率对砂层压密过程的影响可能存在交互性,所以采用全面试验方法,试验测试试样的初始含水率ω0分别为12%,16%,20%,24%,28%;黏性土含量θ分别为10%,20%,30%,40%,50%,测试试样的基本物理参数见表2。
2.2 侧限压缩试验结果分析
不同初始含水率条件下砂层侧限压缩应力-应变曲线如图4所示。
分析图4可知:
表2 试样基本物理参数
Table 2 Basic physical parameters of samples

编号含水率/%黏性土含量/%初始干密度/(g·cm-3)颗粒比重初始孔隙比初始孔隙率/%初始饱和度/%1102.660.8345.438.132202.660.8445.638.18312301.452.670.8445.738.064402.680.8545.937.955502.690.8546.037.836102.660.8345.452.77202.660.8445.652.5816301.452.670.8445.752.39402.680.8545.952.210502.690.8546.052.011102.660.8345.463.912202.660.8445.663.61320301.452.670.8445.763.414402.680.8545.963.215502.690.8546.063.116102.660.8345.476.617202.660.8445.676.41824301.452.670.8445.776.119402.680.8545.975.920502.690.8546.075.721102.660.8345.489.422202.660.8445.689.12328301.452.670.8445.788.824402.680.8545.988.525502.690.8546.088.3

图4 不同初始含水率条件下砂层应力-应变曲线
Fig.4 Stress strain curves of sand layers with different initial water content
(1)砂层压缩过程中应变量随着施加应力的增加而增长,且增长过程呈现显著的非线性特征,在较低应力范围内应变随应力增长迅速,但是在较高应力范围内应变随应力增长速率明显放缓,砂层压缩的困难程度随着压缩过程的进行而不断增加,应力由0 kPa增加至500 kPa即可完成总变形量的35%~75%。
(2)黏性土含量对砂层压缩过程影响显著,随着黏性土含量的增加,砂层在相同应力条件下可达到更大的应变量。当黏性土含量为10%时,最大应变量处于0.08~0.10,当黏性土含量为50%时,最大应变量处于0.19~0.23,增长幅度为130%左右。黏性土颗粒粒径非常细小(<0.075 mm),由于黏性土的双电层效应,其颗粒周围通常包裹着一定厚度的水膜,在压缩过程中水膜可起到一定的润滑作用,使得黏性土颗粒之间发生滑移相对容易,进而表现出较好的可压缩性;而砂颗粒粒径较大(>0.075 mm),在压应力作用下其压缩过程以颗粒之间的错动及变形破坏为主,导致压缩变形的阻力较大,所以砂的可压缩性要显著差于黏性土。含黏性土砂层可看作黏性土与砂的混合物,其力学性状必然受两种成分的共同影响,所以当黏性土含量增加时砂层发生压缩变形变得更容易。
(3)在不同初始含水率条件下,黏性土含量10%和20%对应的ε-p曲线均显著低于黏性土含量30%,40%,50%对应的ε-p曲线,说明黏性土含量对砂层压缩过程的影响具有一定的跳跃性。即相比黏性土含量处于较低水平的砂层,黏性土含量处于较高水平的砂层所对应的可压缩性发生了质变。
原因在于砂层在荷载作用下是否形成了砂骨架,砂骨架的可压缩性远小于黏性土,当黏性土含量较低时,砂层以砂颗粒为主要成分,在侧限压缩过程中很早便形成了砂骨架,砂层的压缩特性由砂骨架控制,砂骨架的存在极大抑制了砂层孔隙的减小,导致整体可压缩性较小(图5(a));当黏性土含量较高时,黏性土颗粒的体积已经超过砂颗粒骨架中的孔隙体积,所以黏性土颗粒不仅会充填砂颗粒之间的孔隙空间,还会导致部分砂颗粒发生分离,导致不能形成砂颗粒骨架,砂层的压缩特性由黏性土控制,最终表现为整体可压缩性较好(图5(b))。所以黏性土含量决定了砂层在侧限压缩过程中是否会形成砂骨架,是否形成砂骨架对于含黏性土砂层来说属于颗粒结构的质变,其必然会引起自身可压缩性能的突变,在图5中表现为黏性土含量10%,20%对应的ε-p曲线均显著低于黏性土含量30%,40%,50%对应的ε-p曲线,因此是否形成砂颗粒骨架的界限黏性土含量必然处于20%~30%,对于青岛地区含黏性土砂层来说,是否形成砂骨架的临界黏性土含量可认为在25%左右。

图5 砂层压缩过程示意
Fig.5 Compression process in sand layer
不同黏性土含量条件下砂层应力-应变曲线如图6所示。分析图6可知:

图6 不同黏性土含量条件下砂层应力-应变曲线
Fig.6 Stress strain curves of sand layers with different clay content
(1)砂层初始含水率对砂层压缩过程有一定影响,但是影响程度没有黏性土含量对压缩曲线的影响显著,不同初始含水率对应的最终应变量最大值与最小值之差在0.018~0.044内,不同黏性土含量对应的最终应变量最大值与最小值之差在0.121~0.134,两者差别较为显著。相比含水率,黏性土含量是砂层压缩过程的主要控制因素。
(2)当初始含水率由12%增加到20%时,砂层压缩量随着含水率的增加而增长,但是当初始含水率由20%增加到28%时,砂层压缩量随着初始含水率的增加而减小,说明初始含水率对砂层压缩过程的影响并非是简单的单调关系,而是存在最优初始含水率,当初始含水率由最优初始含水率增加或者减少时,砂层压缩量都会减小。
分析原因可能为:黏性土具有双电层效应,其颗粒表面包裹着由强结合水和弱结合水构成的水膜,当含水率较低时,黏性土颗粒表面的水膜很薄,颗粒间相互移动需要克服很大的粒间阻力[13],当含水率升高时,黏性土颗粒水膜对黏性土颗粒滑移的润滑作用逐渐显现,同时也对砂颗粒之间的相对移动起到一定的润滑作用,导致砂层压缩量随着含水率的增加而增长。当含水率超过最优含水率后,水膜继续增厚所引起的润滑作用已不明显,但是含水率不断增加时,黏性土中存在与大气隔绝的封闭气泡,且黏性土渗透性小,封闭气泡很难全部被赶走,不利于砂层的压密过程,导致砂层压缩量随着含水率的增加而减小。
3 砂层压密过程数学模型创建
通过观察砂层侧限压缩应力-应变曲线,该曲线通过坐标轴原点,在压缩初始段上升较快,在压缩中后期上升较慢,具有显著的非线性特征。本文采用二次抛物线模型来拟合砂层侧限压缩过程应力-应变曲线(图7),方程形式为
![]()
(1)
式中,ε为砂层应变量;p为砂层所受压应力;A,B,C为表征砂层压密特性的待定常数项,其数值受黏性土含量、初始含水率等影响。

图7 砂层压缩过程数学模型示意
Fig.7 Sketch of model in sand compression process
采用砂层初始压缩模量Es0与p=2 000 kPa时的最终应变量ε2两个特征指标对砂层压缩曲线进行拟合,初始压缩模量可反映砂层压缩初始段的压缩快慢,最终应变量可反映砂层最终的压密程度,Es0,ε2需满足如下条件:① ε-p曲线通过原点(0,0),即![]() ②
②![]() ③ 当p=2 000 kPa时,ε=ε2。
③ 当p=2 000 kPa时,ε=ε2。
上述3个条件可通过方程形式表达:
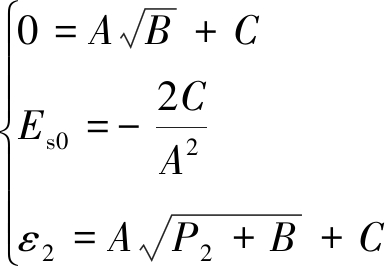
(2)
其中,ε2为p=2 000 kPa时砂层的压缩量;p2=2 000 kPa。求解以上方程可得常数项A,B,C分别为
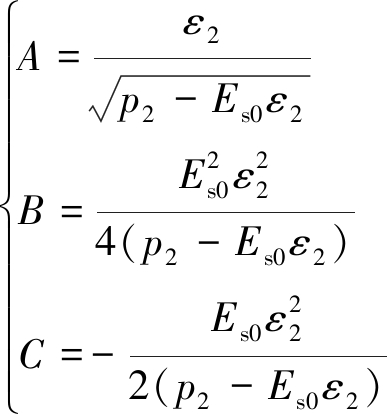
(3)
将常数项代入式(1)可得描述砂层侧限压缩过程的二次抛物线模型的完整形式:
![]()
(4)
式(4)的适用范围为:① 黏性土含量10%~50%,初始含水率12%~28%;② 压力0~2 MPa。相比已有的土体压缩数学模型[12],该公式的优势是可以描述更高压力范围(0~2 MPa)的砂层压缩应力-应变关系,对于砂层注浆工程具有更强的适用性。
砂层压密数学模型中,最终应变量ε2可由试验数据直接得到,初始压缩模量Es0通过0~50 kPa的割线压缩模量确定。砂层初始压缩模量Es0与最终应变量ε2受砂层黏性土含量及初始含水率影响,对于任意黏性土含量及初始含水率条件下的Es0及ε2,可通过已知的Es0及ε2并根据黏性土含量及初始含水率线性插值获取。
4种典型工况下砂层压密过程数学模型曲线与试验数据的对比如图8所示,数学模型曲线与试验数据较为一致,说明所创建的砂层压密数学模型可较好地描述砂层压密过程。

图8 砂层压密过程拟合结果与试验数据对比
Fig.8 Comparison of model results with experimental data
4 砂层压密特性对注浆过程的影响
4.1 劈裂-压密注浆扩散过程计算模型
砂层劈裂-压密注浆扩散过程如图1所示,浆液流型采用宾汉流体模型[15]
![]()
(5)
式中,τ为剪切应力;τ0为初始剪切应力;μ为浆液黏度;![]() 为浆液剪切速率。
为浆液剪切速率。
劈裂通道内部浆液流动在微单元dr上可认为符合裂隙流动规则,根据已有研究成果[16],劈裂通道内部浆液流动方程可表述为
![]()
(6)
式中,p为浆液压力,即砂层所受压应力;r为浆液扩散范围内任意点距离注浆孔的距离;b为与r对应位置处的劈裂通道开度;![]() 为与r对应位置处的浆液平均流速。
为与r对应位置处的浆液平均流速。
在实际劈裂-压密注浆工程中,浆液扩散半径往往在10 m数量级,而浆脉厚度往往在cm数量级,2者相差3个数量级,在受力分析中可认为劈裂通道侧壁与浆液扩散方向平行,劈裂通道侧壁上的浆液压力垂直于浆液扩散方向,劈裂通道两侧砂层只发生垂直于浆液扩散方向的压缩变形,因此在局部范围内可假设砂层压缩过程符合侧限条件,可应用本文提出的砂层压密数学模型来描述砂层的压缩变形。
在未注浆时地层应力较均匀,此时砂层初始应力为σ0,砂层中任意位置处的应变量均为初始应变量ε0,根据式(4),ε0可通过式(7)确定:
![]()
(7)
式中,ε0为砂层初始应变量;σ0为砂层初始应力。
砂层压缩变形与劈裂通道变形满足变形协调条件,在浆液与砂层的接触面上砂层的压缩变形量与劈裂通道开度变化量相等,劈裂通道开度可表示为
b=ΔεD=(ε-ε0)D
(8)
式中,D为劈裂-压密注浆影响范围。
结合式(4),可得劈裂通道开度控制方程:
![]()
(9)
综合浆液流动方程(式(6))与劈裂通道开度控制方程(式(9))可描述砂层劈裂-压密注浆扩散过程中的浆液-砂层应力耦合效应,结合注浆初始条件与边界条件可完整描述注浆扩散过程。
由于式(6)与式(9)无法得到解析解,本文采用文献[17]提出的步进式算法对式(6)与式(9)进行耦合计算,从而获得注浆压力、浆液扩散半径等注浆相关量。
4.2 计算工况
以山东青岛地铁某区段砂层注浆加固工程为背景进行劈裂-压密注浆扩散过程分析,由地层埋深及地层平均重度可获得工程原位初始地应力σ0=306 kPa。考虑到浆液压力对劈裂通道两侧砂层的压缩变形的有效影响范围非常有限,结合工程开挖揭露浆脉情况及模拟试验中浆脉揭露情况[17],综合确定注浆影响范围D=20 cm。相关模拟实验结果表明浆液扩散锋面处的浆脉具有一定厚度值,为了反映该实际情况,参考相关模拟试验结果[17],将浆液扩散锋面处的劈裂通道开度确定为一个较小的数值,在本文中设定该数值为0.2 cm。注浆速率及注浆时间的选择根据依托工程确定,注浆速率取工程实际中的平均注浆速率q=83.4 L/min,注浆时间t=60 min。
黏性土含量是影响砂层压密特性的主控因素,通过调整不同的黏性土含量可获得砂层的不同压密特性,在参考实际工程中砂层黏性土含量范围的基础上,黏性土含量分别设定为θ=10%,20%,30%,3种黏性土含量对应的砂层压缩变形的关键参数A,B,C见表3。
表3 不同黏性土含量对应的砂层压缩变形关键参数
Table 3 Key parameters of compression deformation
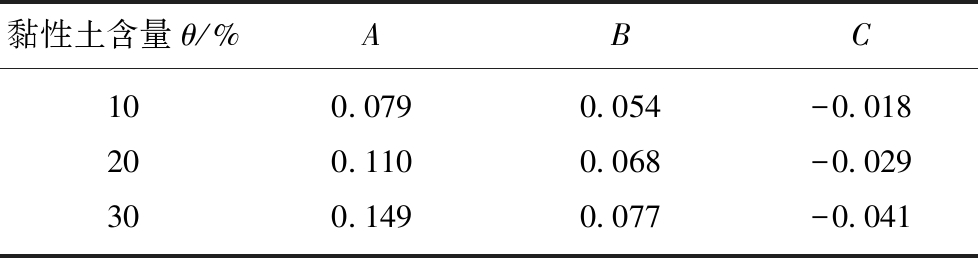
黏性土含量θ/%ABC100.0790.054-0.018200.1100.068-0.029300.1490.077-0.041
选用水灰比W/C=0.8的水泥浆液为典型浆液进行注浆扩散过程分析,W/C=0.8的水泥浆液为宾汉流体[15],其初始剪切应力τ0=5.321 Pa;浆液黏度μ=0.022 9 Pa·s。
4.3 黏性土含量对注浆扩散过程的影响
4.3.1 黏性土含量对劈裂通道开度空间分布的影响
不同黏性土含量条件下劈裂通道开度空间分布对比如图9所示。

图9 不同黏性土含量条件下劈裂通道开度空间分布对比
Fig.9 Spatial distribution of channel opening with different clay contents
分析图9可知:① 劈裂通道开度由注浆孔沿浆液扩散方向衰减,且呈现出明显的非线性特征,劈裂通道开度沿扩散方向的衰减速率慢慢增大,在注浆孔附近衰减较慢,在浆液扩散锋面附近衰减较快。在t=60 min时,最大劈裂通道开度可达到0.6~0.7 cm。② 当砂层黏性土含量增加时,同一时刻注浆孔处的浆脉厚度增加,浆液扩散半径减小,劈裂通道开度在浆液扩散范围内的衰减更快。当黏性土含量由10%增加到30%时,注浆孔处的浆脉厚度大约增加了0.1 cm,浆液扩散半径减小了0.5~2.0 m。由于砂层的可压缩性与黏性土含量正相关,所以在黏性土含量更高的砂层中进行劈裂-压密注浆时,劈裂通道两侧砂层发生压缩变形更容易,最终形成的浆脉厚度较大,但是由于相同时间的总注浆量相同,所以浆液扩散半径相应减小。
4.3.2 黏性土含量对注浆压力的影响
不同黏性土含量条件下注浆压力随时间变化关系对比如图10所示。
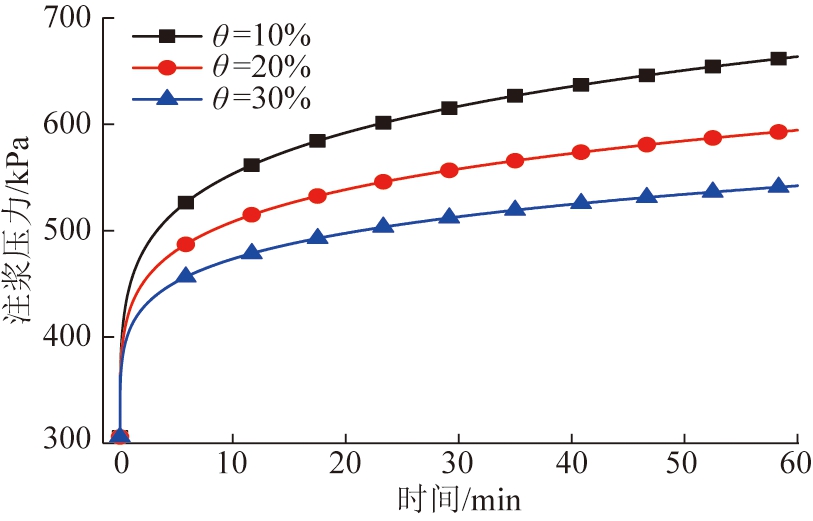
图10 不同黏性土含量条件下注浆压力对比
Fig.10 Comparison of grouting pressure with different clay contents
分析图10可知:① 随着注浆过程的进行,注浆压力由初始地应力306 kPa开始增长,到t=60 min时,注浆压力达到542~664 kPa,注浆压力的增长过程表现出非常显著的非线性特征,在注浆开始阶段注浆压力增长迅速,但是在注浆中后期,注浆压力增长速度逐渐放缓。注浆时间0~6 min,注浆压力增长量可达到总增长量的80%左右,而在中后期注浆压力只是增长了20%左右。② 黏性土含量增加会引起注浆压力增长变慢,θ=30%对应的注浆压力相比θ=10%对应的注浆压力低约120 kPa,相比θ=20%对应的注浆压力低约50 kPa。分析原因为:黏性土含量的增加会导致相同注浆条件下的劈裂通道开度变大,而且扩散半径缩小,由浆液流动方程(式(6))可知,劈裂通道开度变大会减小浆液压力梯度,而浆液扩散半径的减小会导致浆液流动路径变短,两方面都会促使注浆孔处的注浆压力减小。
4.3.3 黏性土含量对浆液扩散半径的影响
不同黏性土含量对浆液扩散半径的影响如图11所示。分析图11可知:① 注浆终压与浆液扩散半径的关系为一个下凹曲线,随着注浆终压的增加,浆液扩散半径也相应增加。当注浆终压处于较低范围时,注浆终压增加引起的浆液扩散半径增加不明显,当注浆终压处于较高范围时,注浆终压增加对浆液扩散半径的影响逐渐增强。② 在相同注浆终压条件下,黏性土含量对浆液扩散半径影响较大,黏性土含量越高,浆液扩散半径也越大,这也反映了黏性土含量增加对于注浆扩散阻力的降低效果。由于高黏性土含量的砂层对应注浆扩散阻力小,所以注浆压力增加慢,若要达到特定的注浆终压,需要的注浆时间更长,因此注浆量更大,最终导致扩散半径大。注浆终压为500 kPa时,θ=20%,30%所对应的浆液扩散半径分别高出θ=10%对应扩散半径的46%及118%。

图11 不同黏性土含量对浆液扩散半径的影响
Fig.11 Influence of clay content on diffusion radius
综上,砂层压密特性可显著影响砂层劈裂-压密注浆扩散过程,当砂层黏性土含量较高时,其可压缩性更高,对浆液扩散的阻力较低,导致在相同注浆时间条件下,黏性土含量与劈裂通道开度正相关,而与浆液扩散半径及注浆压力负相关;在相同注浆终压条件下,黏性土含量与浆液扩散半径正相关。在砂层劈裂-压密注浆设计中应充分考虑砂层压密特性对注浆扩散过程的影响。
5 结 论
(1)黏性土含量是影响砂层压密特性的主控因素,当黏性土含量低于25%左右时,砂层压缩过程中会形成砂骨架,砂层整体可压缩性较差,反之,不会形成砂骨架,砂层整体可压缩性较好。
(2)存在最优初始含水率,当砂层初始含水率由最优初始含水率增加或者减少时,相同压力条件下砂层压缩量都会减小。
(3)建立了可描述砂层非线性压密特征的二次抛物线数学模型,模型参数可通过初始压缩模量及2 MPa下的特征应变量确定,基于该模型可进行砂层劈裂-压密注浆扩散过程的计算。
(4)砂层压密特性对砂层劈裂-压密注浆扩散过程具有显著影响,相同注浆时间条件下,黏性土含量与劈裂通道开度正相关,而与浆液扩散半径及注浆压力负相关;在相同注浆终压条件下,黏性土含量与浆液扩散半径正相关。
[1] 范立民,马雄德,蒋辉,等.西部生态脆弱矿区矿井突水溃沙危险性分区[J].煤炭学报,2016,41(3):531-536.
FAN Limin,MA Xiongde,JIANG Hui,et al.Risk evaluation on water and sand inrush in ecologically fragile coal mine[J].Journal of China Coal Society,2016,41(3):531-536.
[2] HU Zhenqi,CHEN Chao,XIAO Wu,et al.Surface movement and deformation characteristics due to high-intensive coal mining in the windy and sandy region[J].International Journal of Coal Science & Technology,2016,3(3):339-348.
[3] 邝键政,昝月稳,王杰,等.岩土工程注浆理论与工程实例[M].北京:科学出版社,2001.
[4] 袁世冲,张改玲,郑国胜,等.斜井穿越风积砂层水砂突涌注浆治理研究[J].煤炭学报,2018,43(4):1104-1110.
YUAN Shichong,ZHANG Gailing,ZHENG Guosheng,et al.Grouting treatment of water and sand inrush into an inclined shaft in Aeolian sand layer[J].Journal of China Coal Sociery,2018,43(4):1104-1110.
[5] 张庆松,张连震,刘人太,等.基于“浆-土”界面应力耦合效应的劈裂注浆理论研究[J].岩土工程学报,2016,38(2):323-330.
ZHANG Qingsong,ZHANG Lianzhen,LIU Rentai,et al.Split grouting theory based on slurry-soil coupling effects[J].Chinese Journal of Geotechnical Engineering,2016,38(2):323-330.
[6] 李志鹏.断层软弱介质注浆扩散加固机理及工程应用[D].济南:山东大学,2014.
LI Zhipeng.Mechanism of grouting spread and reinforcement on soft medium in fault and its application[D].Jinan:Shandong University,2015.
[7] 邹金锋,李亮,杨小礼.劈裂注浆扩散半径及压力衰减分析[J].水利学报,2006,37(3):314-319.
ZOU Jinfeng,LI Liang,YANG Xiaoli,et al.Penetration radius and pressure attenuation law in fracturing grouting[J].Journal of Hydraulic Engineering,2006,37(3):314-319.
[8] 孙锋,陈铁林,张顶立,等.基于宾汉体浆液的海底隧道劈裂注浆机制研究[J].北京交通大学学报(自然科学版),2009,33(4):1-6.
SUN Feng,CHEN Tielin,ZHANG Dingli,et al.Study on fracture grouting mechanism in subsea tunnel based on Bingham fluids[J].Journal of Beijing Jiaotong University,2009,33(4):1-6.
[9] 孙锋,张顶立,陈铁林.基于流体时变性的隧道劈裂注浆机制研究[J].岩土工程学报,2011,33(1):88-93.
SUN Feng,ZHANG Dingli,CHEN Tielin.Fracture grouting mechanism in tunnels based on time-dependent behaviors of grout[J].Chinese Journal of Geotechnical Engineering,2011,33(1):88-93.
[10] 张忠苗,邹健.桩底劈裂注浆扩散半径和注浆压力研究[J].岩土工程学报,2008,30(2):181-184.
ZHANG Zhongmiao,ZOU Jian.Penetration radius and grouting pressure in fracture grouting[J].Chinese Journal of Geotechnical Engineering,2008,30(2):181-184.
[11] 冯强,刘炜炜,付圣岗,等.基于弹性地基梁采场坚硬顶板变形与内力的解析计算[J].采矿与安全工程学报,2017,34(2):342-347.
FENG Qiang,LIU Weiwei,FU Shenggang,et al.Analytical solution for deformation and internal force of hard roof in stope based on elastic foundation beam[J].Journal of Mining & Safety Engineering,2017,34(2):342-347.
[12] 张连震,李志鹏,张庆松,等.基于土体非线性压密效应的劈裂注浆机制分析[J].岩石力学与工程学报,2016,35(7):1483-1493.
ZHANG Lianzhen,LI Zhipeng,ZHANG Qingsong,et al.Split grouting mechanism based on nonlinear characteristics of compression process of soil[J].Chinese Journal of Rock Mechanics and Engineering,2016,35(7):1483-1493.
[13] 李广信.高等土力学[M].北京:清华大学出版社,2004.
[14] 中华人民共和国建设部.GB/T 50123—1999 土工试验方法标准[S].北京:中国计划出版社,1999.
[15] 阮文军.基于浆液粘度时变性的岩体裂隙注浆扩散模型[J].岩石力学与工程学报.2005,24(15):2709-2714.
RUAN Wenjun.Spreading model of grouting in rock mass fissures based on time-dependent behavior of viscosity of cement-based grouts[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(15):2709-2714.
[16] 张庆松,张连震,张霄,等.基于浆液黏度时空变化的水平裂隙岩体注浆扩散机制[J].岩石力学与工程学报.2015,34(6):1198-1210.
ZHANG Qingsong,ZHANG Lianzhen,ZHANG Xiao,et al.Grouting diffusion in a horizontal crack considering temporal and spatial variation of viscosity[J].Chinese Journal of Rock Mechanics and Engineering,2015,34(6):1198-1210.
[17] 张连震.地铁穿越砂层注浆扩散与加固机制及工程应用[D].济南:山东大学,2017.
ZHANG Lianzhen.Study on penetration and reinforcement mechanism of grouting in sand layer disclosed by subway tunnel and its application[D].Jinan:Shandong University,2017.
